Question

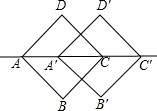如图，把正方形ABCD沿着对角线AC的方向移动到正方形A′B′C′D′的位置，它们的重叠部分的面积是正方形ABCD面积的一半，若AC=

2

，则正方形移动的距离AA′为（　　）

• A、

  2

• B、1
• C、

  2

  -1
• D、1-

  2

Answer 1

分析：因为重叠部分的面积是正方形ABCD面积的一半，所以根据相似比可知A′C：AC=1：

2

，即可得AA′=

2

-1．

解答：解：∵重叠部分的面积是正方形ABCD面积的一半，即重叠部分与正方形的面积的比是1：2．则相似比是1：

2

．
∴A′C：AC=1：

2

，
∵AC=

2

，
∴AA′=AC-A′C=

2

-1．
故选C．

点评：主要考查了正方形的性质和中位线的性质以及相似三角形中的相似比．要注意，相似形的面积比是相似比的平方．