Question

【题目】已知BD、CE是△ABC的两条高，直线BD、CE相交于点H．
（1）若∠A=100°，如图，求∠DHE的度数；
（2）若△ABC中∠A=50°，直接写出∠DHE的度数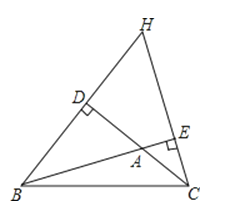

Answer 1

【答案】解：（1）∵BD、CE是△ABC的两条高，
∴∠HDA=∠HEA=90°，
∴∠DHE=180°﹣∠A=80°；
（2）当∠A=50°时，
①△ABC是锐角三角形时，∠DHE=180°﹣50°=130°；
②△ABC是钝角三角形时，∠DHE=∠A=50°；
故答案为：50°或130°．
【解析】（1）根据四边形的内角和是360°，求得∠DHE的度数；
　　　　（2）分∠A是锐角时△ABC是锐角三角形，钝角三角形讨论求解即可．
【考点精析】解答此题的关键在于理解三角形的内角和外角的相关知识，掌握三角形的三个内角中，只可能有一个内角是直角或钝角；直角三角形的两个锐角互余；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角．