题目内容
【题目】如图,OE平分∠AOB,且EC⊥OA,ED⊥OB,垂足分别是C,D,连结CD与OE交于点F.
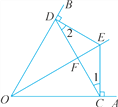
(1)求证:∠1=∠2.
(2)求证:OE是线段CD的垂直平分线.
(3)若∠1=30°,OC=2,求△OCD与△CDE的面积之差.
【答案】(1)证明见解析(2)证明见解析(3)![]()
【解析】试题分析:(1)根据角平分线上的点到角的两边的距离相等可得CE=DE,然后根据等边对等角证明即可;
(2)利用“HL”证明△OCE和△ODE全等,根据全等三角形对应边相等可得OC=OD,再根据到线段两端点距离相等的点在线段垂直平分线上证明.
(3)分别求出ΔOCD和ΔCDE的面积即可求出△OCD与△CDE的面积之差.
试题解析:(1)∵OE平分∠AOB,EC⊥OA,ED⊥OB,
∴CE=DE,∴∠1=∠2.
(2)在Rt△OCE和Rt△ODE中,
∵![]()
∴Rt△OCE≌Rt△ODE(HL).
∴OC=OD.
又∵CE=DE,
∴OE是线段CD的垂直平分线.
(3)∵∠1=30°,∠OCE=90°,
∴∠OCD=60°.
∵OC=OD,
∴△OCD是边长为2的等边三角形,
∴CD=OC=2,∠COD=60°,
∴∠COE=∠DOE=![]() ∠COD=30°,
∠COD=30°,
∴OE=2CE.
设CE=x,则OE=2x.
由勾股定理,得(2x)2=x2+22,
解得x=![]() ,即CE=
,即CE=![]() ,OE=
,OE=![]() .
.
∵∠1=30°,∠EFC=90°,
∴EF=![]() CE=
CE=![]() ,∴OF=OE-EF=
,∴OF=OE-EF=![]() ,
,
∴S△OCD-S△CDE=![]() ·CD·OF-
·CD·OF-![]() ·CD·EF=
·CD·EF=![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目