Question

【题目】如图，在△ABC中，点D、E分别是边BC、AC的中点，过点A作AF∥BC交DE的延长线于点F，连接CF。

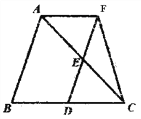
（1）求证：四边形ABDF是平行四边形；

（2）若∠CAF=45°，BC=4，CF=，求AB的长。

Answer 1

【答案】（1）证明见解析；

（2）AB的长为

【解析】分析：（1）求出DE∥AB，AF∥BC来证明四边形ABDF是平行四边形．

（2）过点F作FG⊥AC于G点，求出AC和GF的长再求△CAF的面积．

本题解析：

证明：（1）在△ABC中，点D、E分别是边BC、AC的中点，

∴DE∥AB， 又知AF∥BC，∴四边形ABDF是平行四边形。

（2）过点F作FG交AC于点G，过点A作AH交BC于点H。

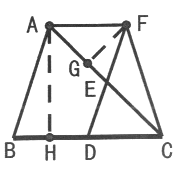
∵FG⊥AC，∴∠AGF=90°，∵∠CAF=45°，由（1）知，四边形ABDF是平行四边形，

∴AF=BD=BC=2，在RT△AFG中，∠CAF=45°，∴AG=GF=AF=。在RT△CFG中，CF=，

∴CG=，∵AF∥BC，∴∠ACB=45°，

∵AH⊥BC，在RT△ACH中，AC=AG+GC=+2=3，∴AH=HC=×3=3，

∴BH=BC-CH=4-3=1。在RT△ABH中，AB=.