题目内容
已知一次函数 的图象经过点
的图象经过点 ,且与函数
,且与函数 的图象相交于点
的图象相交于点 .
.
(1)求 的值;
的值;
(2)若函数 的图象与
的图象与 轴的交点是B,函数
轴的交点是B,函数 的图象与
的图象与 轴的交点是C,求四边形
轴的交点是C,求四边形 的面积(其中O为坐标原点).
的面积(其中O为坐标原点).
 的图象经过点
的图象经过点 ,且与函数
,且与函数 的图象相交于点
的图象相交于点 .
.(1)求
 的值;
的值;(2)若函数
 的图象与
的图象与 轴的交点是B,函数
轴的交点是B,函数 的图象与
的图象与 轴的交点是C,求四边形
轴的交点是C,求四边形 的面积(其中O为坐标原点).
的面积(其中O为坐标原点).(1)a= ;(2)SABOC=
;(2)SABOC= .
.
 ;(2)SABOC=
;(2)SABOC= .
.试题分析:(1)根据一次函数y=kx+b的图象与函数
 的图象相交于点
的图象相交于点 ,先求a的值,
,先求a的值,(2)再把A、P两点的坐标代入一次函数y=kx+b中,求得k、b的值,再由题意求得B、C两点的坐标,从而求出四边形ABOC的面积
试题解析:
(1)由题意将A坐标代入
 得:a=
得:a=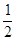 ×
× +1=
+1=
(2)∵直线y=kx+b过点P(0,?3),A(
 ,
, ),
),∴
 ,解得
,解得
∴函数y=2x-3的图象与x轴的交点B(
 ,0)
,0)函数
 的图象与y轴的交点C(0,1)
的图象与y轴的交点C(0,1)又S△ACP=
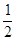 ×4×
×4× =
= ,S△BOP=
,S△BOP=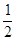 ×3×
×3× =
= ,(7分)
,(7分)∴SABOC=S△ACP?S△BOP=
 ?
? =
= .(8分)
.(8分)
练习册系列答案
相关题目
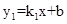 的图象与函数
的图象与函数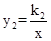 (
(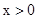 )的图象交于点A(2,1)、B,与y轴交于点C(0,3).
)的图象交于点A(2,1)、B,与y轴交于点C(0,3).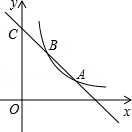
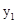 的表达式和点B的坐标;
的表达式和点B的坐标;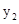 的大小.
的大小.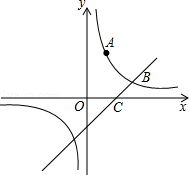
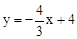 的图象与x轴、y轴分别相交于点A、B.P是射线BO上的一个动点(点P不与点B重合),过点P作PC⊥AB,垂足为C,在射线CA上截取CD=CP,连接PD.设BP=t.
的图象与x轴、y轴分别相交于点A、B.P是射线BO上的一个动点(点P不与点B重合),过点P作PC⊥AB,垂足为C,在射线CA上截取CD=CP,连接PD.设BP=t.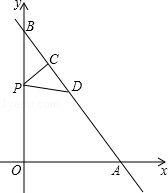
 、
、 在直线
在直线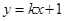 上,且
上,且 ,则该直线所经过的象限是……( )
,则该直线所经过的象限是……( )