题目内容
如图,在□ABCD中,点E,F分别在边DC,AB上,DE=BF,把平行四边形沿直线EF折叠,使得点B,C分别落在点B′,C′处,线段EC′与线段AF交于点G,连接DG,B′G。

求证:(1)∠1=∠2 (2)DG=B′G

求证:(1)∠1=∠2 (2)DG=B′G
见解析
证明:(1)∵在平行四边形ABCD中,DC∥AB,
∴∠2=∠FEC。
由折叠得:∠1=∠FEC,∴∠1=∠2。
(2)∵∠1=∠2,∴EG=GF。
∵AB∥DC,∴∠DEG=∠EGF。
由折叠得:EC′∥B′F,∴∠B′FG=∠EGF。
∵DE=BF=B′F,∴DE=B′F,。
∴△DEG≌△B′FG(AAS)。∴DG=B′G。
(1)根据平行四边形得出DC∥AB,推出∠2=∠FEC,由折叠得出∠1=∠FEC=∠2,即可得出答案。
(2)求出EG=B′G,推出∠DEG=∠EGF,由折叠求出∠B′FG=∠EGF,求出DE=B′F,证△DEG≌△B′FG即可。
∴∠2=∠FEC。
由折叠得:∠1=∠FEC,∴∠1=∠2。
(2)∵∠1=∠2,∴EG=GF。
∵AB∥DC,∴∠DEG=∠EGF。
由折叠得:EC′∥B′F,∴∠B′FG=∠EGF。
∵DE=BF=B′F,∴DE=B′F,。
∴△DEG≌△B′FG(AAS)。∴DG=B′G。
(1)根据平行四边形得出DC∥AB,推出∠2=∠FEC,由折叠得出∠1=∠FEC=∠2,即可得出答案。
(2)求出EG=B′G,推出∠DEG=∠EGF,由折叠求出∠B′FG=∠EGF,求出DE=B′F,证△DEG≌△B′FG即可。

练习册系列答案
相关题目
 ABCD中,F是AD的中点,延长BC到点E,使CE=
ABCD中,F是AD的中点,延长BC到点E,使CE=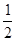 BC,连结DE,CF。
BC,连结DE,CF。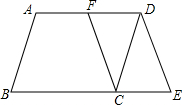
 ABCD中,下列结论一定正确的是
ABCD中,下列结论一定正确的是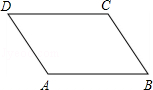
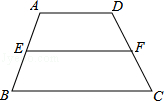
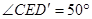 ,则
,则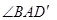 的大小是
的大小是 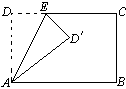
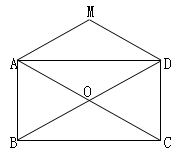
 的正方形的中心
的正方形的中心 为端点,引两条相互垂直的射线,分别与正方形的两邻边交于
为端点,引两条相互垂直的射线,分别与正方形的两邻边交于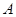 、
、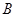 两点,则线段
两点,则线段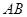 的最小值是 .
的最小值是 .