��Ŀ����
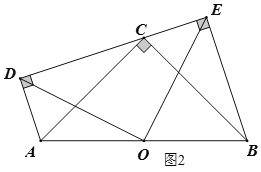
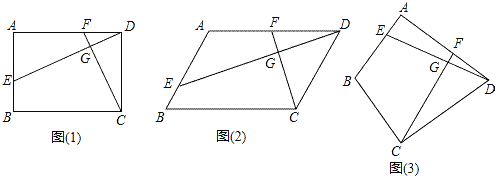
����Ŀ����֪�ı���ABCD�У�E��F�ֱ���AB��AD���ϵĵ㣬DE��CF���ڵ�G��
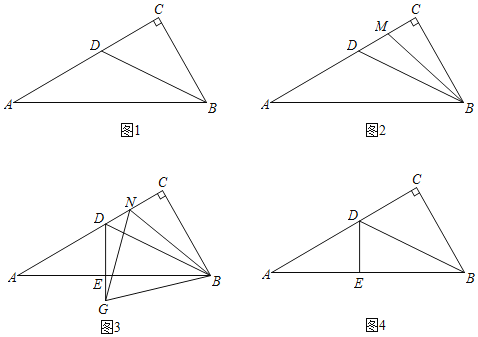
(1)��ͼ1�����ı���ABCD�Ǿ��Σ���DE��CF����DECD�� ��CFAD��������������=��������������
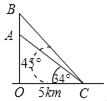
(2)��ͼ2�����ı���ABCD��ƽ���ı��Σ���̽��������B���EGC����ʲô��ϵʱ��ʹ��DECD=CFAD��������֤����Ľ��ۣ�
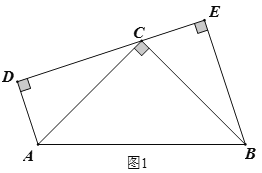
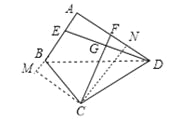
(3)��ͼ3����BA=BC=3��DA=DC=4����BAD=90�㣬DE��CF����![]() ��ֵΪ�� ����
��ֵΪ�� ����
���𰸡�(1)=��(2)����B+��EGC=180��ʱ��DECD=CFAD������֤����������(3)![]() ��
��
��������
���⣨1�����ݾ������ʵó���A=��FDC=90���������CFD=��AED��֤����AED�ס�DFC���ɣ�
��2������B+��EGC=180��ʱ��![]() ������֤��DFG�ס�DEA���ó�
������֤��DFG�ס�DEA���ó�![]() ��֤��CGD�ס�CDF���ó�
��֤��CGD�ס�CDF���ó�![]() �����ɵó��𰸣�
�����ɵó��𰸣�
��3����C��CN��AD��N��CM��AB��AB�ӳ�����M������BD����CN=x����BAD�ա�BCD���Ƴ���BCD=��A=90����֤��BCM�ס�DCN�����CM=x����Rt��CMB�У��ɹ��ɶ����ó�![]() ������ó�����
���������![]() �����CN=
�����CN=![]() ��֤����AED�ס�NFC�����ɵó��𰸣�
��֤����AED�ס�NFC�����ɵó��𰸣�
�����������1��֤�������ı���ABCD�Ǿ��Σ�
���A=��FDC=90����
��CF��DE��
���DGF=90����
���ADE+��CFD=90������ADE+��AED=90����
���CFD=��AED��
�ߡ�A=��CDF��
���AED�ס�DFC��
��![]() ����
����![]() =
=![]() .
.
��2������B+��EGC=180��ʱ��![]() =
=![]() ������
������
֤�������ı���ABCD��ƽ���ı��Σ�
���B=��ADC��AD��BC��
���B+��A=180����
�ߡ�B+��EGC=180����
���A=��EGC=��FGD��
�ߡ�FDG=��EDA��
���DFG�ס�DEA��
��![]() ��
��
�ߡ�B=��ADC����B+��EGC=180������EGC+��DGC=180����
���CGD=��CDF��
�ߡ�GCD=��DCF��
���CGD�ס�CDF��
��![]() ��
��
��![]() ��
��
��![]() ��
��
������B+��EGC=180��ʱ��![]() ������
������
��3���⣺![]() ��
��
�����ǣ���C��CN��AD��N��CM��AB��AB�ӳ�����M������BD����CN=x��
��AB��AD��
���A=��M=��CNA=90����
���ı���AMCN�Ǿ��Σ�
��AM=CN��AN=CM��
������BAD����BCD��
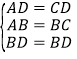
���BAD�ա�BCD��SSS����
���BCD=��A=90����
���ABC+��ADC=180����
�ߡ�ABC+��CBM=180����
���CBM=��ADC��
�ߡ�CND=��M=90����
���BCM�ס�DCN��
��![]() ��
��
��![]()
��![]()
��Rt��CMB�У�![]() ��BM=AM��AB=x��6���ɹ��ɶ����ã�
��BM=AM��AB=x��6���ɹ��ɶ����ã�![]() ��
��
��![]() ��
��
��� x=0����ȥ����x=![]()
��CN=![]() ��
��
�ߡ�A=��FGD=90����
���AED+��AFG=180����
�ߡ�AFG+��NFC=180����
���AED=��CFN��
�ߡ�A=��CNF=90����
���AED�ס�NFC��
��![]()
����: �����������ۺ���.

����Ŀ��ij��ѧ����С����������ѹǿʵ��ʱ�����ѹǿp(Pa)�����V(cm3)֮�������ж�Ӧ���ݣ�
p(Pa) | �� | 1 | 2 | 3 | 4 | 5 | �� |
V(cm3) | �� | 6 | 3 | 2 | 1.5 | 1.2 | �� |
���ݱ����ṩ����Ϣ���ش��������⣺
(1)����p��V֮��Ĺ�ϵ�������������ϵʽ��
(2)������������12cm3ʱ��ѹǿ�Ƕ��٣�