题目内容
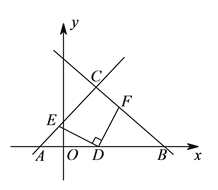
【题目】如图,在平面直角坐标系中,已知直线![]() 和
和![]() 与
与![]() 轴分别相交于点
轴分别相交于点![]() 和点
和点![]() ,设两直线相交于点
,设两直线相交于点![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 上一个动点(不与点
上一个动点(不与点![]() 和
和![]() 重合),连结
重合),连结![]() ,并过点
,并过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
(![]() )判断
)判断![]() 的形状,并说明理由.
的形状,并说明理由.
(![]() )当点
)当点![]() 在线段
在线段![]() 上运动时,四边形
上运动时,四边形![]() 的面积是否为定值?若是,请求出这个定值;若不是,请说明理由.
的面积是否为定值?若是,请求出这个定值;若不是,请说明理由.
(![]() )当点
)当点![]() 的横坐标为
的横坐标为![]() 时,在
时,在![]() 轴上找到一点
轴上找到一点![]() 使得
使得![]() 的周长最小,请直接写出点
的周长最小,请直接写出点![]() 的坐标.
的坐标.
【答案】(![]() )等腰直角三角形,理由见解析;(
)等腰直角三角形,理由见解析;(![]() )定值为8;(
)定值为8;( ![]() )
)![]()
【解析】试题分析:(1)分别求出A、B、C三点坐标以及AC、AB、BC的长,即可得出![]() 的形状;
的形状;
(2)![]() ,可知四边形
,可知四边形![]() 的面积是定值;
的面积是定值;
(3)利用轴对称的性质即可求解.
解:(![]() )由题意可知
)由题意可知![]() ,
, ![]() ,令
,令![]() ,则
,则![]() ,
, ![]() ,
,
∴![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,则
,则![]() ,且
,且![]() ,
,
∴![]() 为等腰直角三角形.
为等腰直角三角形.
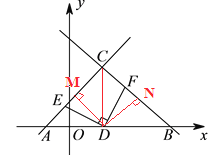
(![]() )由题意知
)由题意知![]() ,即
,即![]() ,连结
,连结![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,
, ![]() 于
于![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() ,
, ![]() 平分
平分![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
∴![]() ,是定值.
,是定值.
(![]() )当
)当![]() 时,
时, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴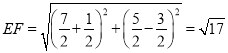 ,
,
则要使![]() 周长最小,即只需时
周长最小,即只需时![]() 最小,又两点之间线段最短,
最小,又两点之间线段最短,
∴设![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,
,
∴![]() ,令
,令![]() ,
, ![]() ,
,
∴![]() .
.

练习册系列答案
相关题目
【题目】如图,均匀的正四面体的各面依次标有1,2,3,4四个数字.小明做了60次投掷试验,结果统计如下:

朝下数字 | 1 | 2 | 3 | 4 |
出现的次数 | 16 | 20 | 14 | 10 |
【1】计算上述试验中“4朝下”的频率是_________
【2】根据试验结果,投掷一次正四面体,出现2朝下的概率是![]() .”的说法正确吗?为什么?
.”的说法正确吗?为什么?
【3】随机投掷正四面体两次,请用列表或画树状图法,求两次朝下的数字之和大于4的概率.




