题目内容
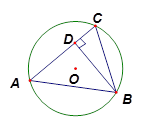
如图,点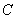 是半圆
是半圆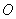 的半径
的半径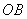 上的动点,作
上的动点,作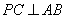 于
于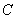 .点
.点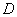 是半圆上位于
是半圆上位于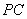 左侧的点,连结
左侧的点,连结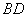 交线段
交线段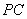 于
于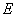 ,且
,且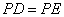 .
.

(1)求证: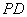 是⊙O的切线.
是⊙O的切线.
(2)若⊙O的半径为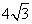 ,
,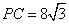 ,设
,设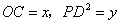 .
.
①求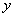 关于
关于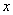 的函数关系式.
的函数关系式.
②当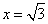 时,求
时,求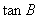 的值.
的值.
 是半圆
是半圆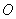 的半径
的半径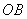 上的动点,作
上的动点,作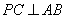 于
于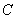 .点
.点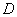 是半圆上位于
是半圆上位于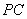 左侧的点,连结
左侧的点,连结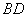 交线段
交线段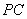 于
于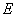 ,且
,且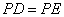 .
.
(1)求证:
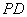 是⊙O的切线.
是⊙O的切线.(2)若⊙O的半径为
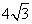 ,
,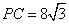 ,设
,设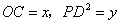 .
.①求
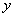 关于
关于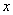 的函数关系式.
的函数关系式.②当
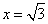 时,求
时,求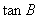 的值.
的值.(1)连接DO,根据垂直的定义可得∠3+∠4=90°,由PD=PE,OD=OB可得∠1=∠2,∠5=∠4,又∠2=∠3可得∠1+∠5=90°,即得∠PDO=90°,从而证得结论;(2)①y=x2+144;②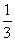
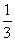
试题分析:(1)连接DO,根据垂直的定义可得∠3+∠4=90°,由PD=PE,OD=OB可得∠1=∠2,∠5=∠4,又∠2=∠3可得∠1+∠5=90°,即得∠PDO=90°,从而证得结论;
(2)①连接PO,在Rt△PDO中PD2=y,DC=4
 ,则PO2=y+(4
,则PO2=y+(4 )2=y+48,在Rt△PCO中OC="x" PC=8
)2=y+48,在Rt△PCO中OC="x" PC=8 ,则可得PO2=x2+(8
,则可得PO2=x2+(8 )2=x2+192 ,所以有y+48=x2+192,从而求得结果;
)2=x2+192 ,所以有y+48=x2+192,从而求得结果;②当x=
 时,可得y=147,即可得到PD、PE的长,由PC=8
时,可得y=147,即可得到PD、PE的长,由PC=8 可得EC的长,又OC=X=
可得EC的长,又OC=X= ,OB=4
,OB=4 可得CB=3
可得CB=3 ,在Rt△BCE中,根据正切函数的定义求解即可.
,在Rt△BCE中,根据正切函数的定义求解即可.(1)连接DO
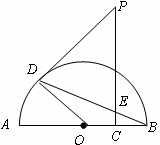
∵PC⊥BA
∴∠PCB=90°
∴∠3+∠4=90°
又∵PD=PE,OD=OB
∴∠1=∠2,∠5=∠4
又∵∠2=∠3
∴∠1+∠5=90°
∴∠PDO=90°
∴PD⊥OD
∴PD是QO切线;
(2)①连接PO
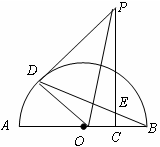
在Rt△PDO中PD2=y,DC=4

∴PO2=y+(4
 )2="y+48"
)2="y+48" 在Rt△PCO中OC=x,PC=8

∴PO2=x2+(8
 )2=x2+192
)2=x2+192 ∴y+48=x2+192
∴y=x2+144
②当x=
 时,y=147
时,y=147∴PD=
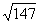 =7
=7
∴PE=PD=7

∵PC=8

∴EC=8
 -7
-7 =
=
又∵OC=x=
 ,OB=4
,OB=4
∴CB=3

在Rt△BCE中,tanB=
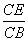 =
=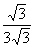 =
=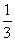 .
.点评:圆的综合题是初中数学的重点和难点,在中考中极为常见,一般以压轴题形式出现,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,矩形CDEF内接于半圆,点C,D在AB上,点E,F在半圆上.
,矩形CDEF内接于半圆,点C,D在AB上,点E,F在半圆上.
 ︰2时,求弧AF的度数;
︰2时,求弧AF的度数;
 和弦AC的长.(弧长计算结果保留
和弦AC的长.(弧长计算结果保留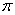 )
)
 ,侧面展开图是半圆,则圆锥的侧面积是( )
,侧面展开图是半圆,则圆锥的侧面积是( )
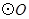 的半径为
的半径为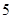 ,锐角
,锐角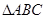 内接于
内接于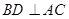 于点
于点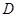 ,
,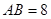 , 则
, 则