题目内容
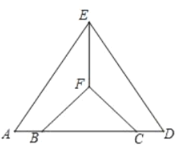
【题目】如图,点A,B,C,D在同一条直线上,AB=DC,在四个论断“EA=ED,EF⊥AD,AB=DC,FB=FC”中选择二个作为已知条件,另一个作为结论,构成真命题(补充已知和求证),并进行证明.
已知、如图,点A,B,C,D在同一条直线上, .
求证、 .
证明、 .
【答案】见解析
【解析】
已知:EA=ED,EF⊥AD,AB=DC,求证FB=FC.想办法证明EF是线段BC的垂直平分线即可.(答案不唯一)
已知:如图,EA=ED,EF⊥AD,AB=DC,求证FB=FC.
理由:延长EF交BC于H.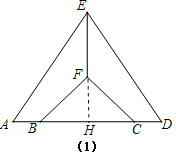
∵EA=ED,EF⊥AD,
∴AH=HD,
∵AB=DC,
∴BH=CH,∵FH⊥BC,
∴FB=FC.
故答案为:EA=ED,EF⊥AD,AB=DC;FB=FC;
延长EF交BC于H.
∵EA=ED,EF⊥AD,
∴AH=HD,
∵AB=DC,
∴BH=CH,∵FH⊥BC,
∴FB=FC.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目