题目内容
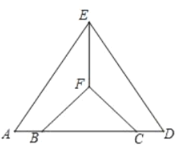
【题目】如图,Rt△ABC中,∠ACB=90°,AC=BC,CF交AB于E,BD⊥CF,AF⊥CF,则下列结论:①∠ACF=∠CBD②BD=FC③FC=FD+AF④AE=DC中,正确的结论是____________(填正确结论的编号)

【答案】①②③
【解析】
根据同角的余角相等,可得到结论①,再证明△ACF≌△CBD,然后根据全等三角形的性质判断结论②、③、④即可.
解:∵BD⊥CF,AF⊥CF,
∴∠BDC=∠AFC=90°,
∵∠ACB=90°,
∴∠ACF+∠BCD=∠CBD+∠BCD=90°,
∴∠ACF=∠CBD,故①正确;
在△ACF和△CBD中,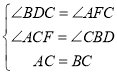 ,
,
∴△ACF≌△CBD,
∴BD=FC,CD=AF,故结论②正确
∴FC=FD+CD=FD+AF,故结论③正确,
∵在Rt△AEF中,AE>AF,
∴AE>CD,故结论④错误.
综上所述,正确的结论是:①②③.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目