题目内容
 22、如图,已知△DAC和△ECB是两个大小不同的等边三角形,点A、C、B在同一直线上,AE、BD分别与CD、CE交于点M、N.
22、如图,已知△DAC和△ECB是两个大小不同的等边三角形,点A、C、B在同一直线上,AE、BD分别与CD、CE交于点M、N.(1)试说明:△ACE≌△DCB;
(2)连接MN,则MN∥AB,请说明理由.
分析:(1)欲证三角形全等,利用全等的条件进行判定即可;因为△DAC和△ECB均为等边三角形,即有∠ACD=∠ECB=60°,即∠ACD+∠DCN=∠ECB+∠DCN,即可得出∠ACE=∠DCB,再利用边的关系,即可得正△ACE≌△DCB(SAS);
(2)由(1)可知,△ACE≌△DCB(SAS),即有∠MEC=∠NBC,从而可得∠MCN=60°,又因为∠MCN=∠ECB,且EC=CB,
即证△MCE≌△NCB从而可推出,即有∠CNM+∠CAN=120°,即证MN∥AB
(2)由(1)可知,△ACE≌△DCB(SAS),即有∠MEC=∠NBC,从而可得∠MCN=60°,又因为∠MCN=∠ECB,且EC=CB,
即证△MCE≌△NCB从而可推出,即有∠CNM+∠CAN=120°,即证MN∥AB
解答: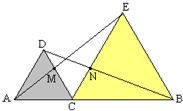 解:(1)∵∠ACD=∠ECB=60°,∴∠ACD+∠DCN=∠ECB+∠DCN,
解:(1)∵∠ACD=∠ECB=60°,∴∠ACD+∠DCN=∠ECB+∠DCN,
∴∠ACE=∠DCB,∵AC=DC,EC=BC,
∴△ACE≌△DCB(SAS)
(2)∵△ACE≌△DCB(SAS),∴∠MEC=∠NBC,
∵∠MCN=180°-∠ACD-∠ECB=60°,∴∠MCN=∠ECB,∵EC=CB,
∴△MCE≌△NCB,∴MC=NC,∴∠CNM=60°,∴∠CNM+∠CAN=120°,∴MN∥AB
 解:(1)∵∠ACD=∠ECB=60°,∴∠ACD+∠DCN=∠ECB+∠DCN,
解:(1)∵∠ACD=∠ECB=60°,∴∠ACD+∠DCN=∠ECB+∠DCN,∴∠ACE=∠DCB,∵AC=DC,EC=BC,
∴△ACE≌△DCB(SAS)
(2)∵△ACE≌△DCB(SAS),∴∠MEC=∠NBC,
∵∠MCN=180°-∠ACD-∠ECB=60°,∴∠MCN=∠ECB,∵EC=CB,
∴△MCE≌△NCB,∴MC=NC,∴∠CNM=60°,∴∠CNM+∠CAN=120°,∴MN∥AB
点评:本题主要考查了等边三角形的性质和全等三角形的判定和性质,属于中等题目,要求学生具备一定的几何知识和解题能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
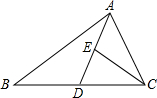 如图,已知,AD是ABC的中线,且∠DAC=∠B,CD=CE.
如图,已知,AD是ABC的中线,且∠DAC=∠B,CD=CE.
 如图,已知△DAC和△ECB是两个大小不同的等边三角形,点A、C、B在同一直线上,AE、BD分别与CD、CE交于点M、N.
如图,已知△DAC和△ECB是两个大小不同的等边三角形,点A、C、B在同一直线上,AE、BD分别与CD、CE交于点M、N.