题目内容
21、如图，已知△ABC．
（1）画出△ABC的高AD．
（2）若AE、BF分别是△ABC的角平分线，且AE、BF交于点O，请补全图形．（只要求画出示意图）
（3）在（1）和（2）的条件下，若∠A=60°，∠C=70°，求∠DAC、∠DAE、∠BOA的度数．
（1）画出△ABC的高AD．
（2）若AE、BF分别是△ABC的角平分线，且AE、BF交于点O，请补全图形．（只要求画出示意图）
（3）在（1）和（2）的条件下，若∠A=60°，∠C=70°，求∠DAC、∠DAE、∠BOA的度数．
分析：（1）过点A作BC的垂线AD，交BC于D；
（2）作∠A和∠B的角平分线AE、BF交于点O；
（3）根据直角三角形的两锐角互余，可得∠DAC=20°，根据角平分线的定义，可求得∠DAE=10°；根据三角形外角的性质，可求得∠BOA=125°．
（2）作∠A和∠B的角平分线AE、BF交于点O；
（3）根据直角三角形的两锐角互余，可得∠DAC=20°，根据角平分线的定义，可求得∠DAE=10°；根据三角形外角的性质，可求得∠BOA=125°．
解答：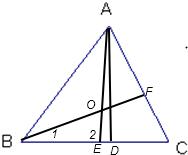
解：（1）（2）如图．
（3）∵AD⊥BC，∠C=70°，
∴∠DAC=90°-70°=20°，
∵AE平分∠BAC，∠BAC=60°，
∴∠EAC=30°，
∴∠DAE=30°-20°=10°，
∴∠2=∠EAC+∠C=30°+70°=100°，
∵∠1=（180°-60°-70°）÷2=25°，
∴∠BOA=∠1+∠2=25°+100°=125°．
解：（1）（2）如图．（3）∵AD⊥BC，∠C=70°，
∴∠DAC=90°-70°=20°，
∵AE平分∠BAC，∠BAC=60°，
∴∠EAC=30°，
∴∠DAE=30°-20°=10°，
∴∠2=∠EAC+∠C=30°+70°=100°，
∵∠1=（180°-60°-70°）÷2=25°，
∴∠BOA=∠1+∠2=25°+100°=125°．
点评：此题是计算与作图相结合的探索．考查学生运用作图工具的能力，以及运用直角三角形、三角形内角与外角等基础知识解决问题的能力．
练习册系列答案
冲刺100分1号卷系列答案
相关题目
24、如图，已知△ABC和△CDE均为等边三角形，且点B、C、D在同一条直线上，连接AD、BE，交CE和AC分别于G、H点，连接GH．
如图，已知△ABC，∠ACB=90°，AC=BC，点E、F在AB上，∠ECF=45°．
17、（1）已知线段a，h，用直尺和圆规作等腰三角形ABC，底边BC=a，BC边上的高为h（要求尺规作图，不写作法和证明）
20、如图，已知△ABC是锐角三角形，且∠A=50°，高BE、CF相交于点O，求∠BOC的度数．