题目内容
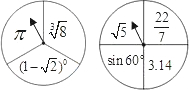 如图所示的两个转盘分别被均匀地分成3个和4个扇形,每个扇形上都标有一个实数.同时自由转动两个转盘,转盘停止后(若指针指在分格线上,则重转),两个指针都落在无理数上的概率是( )
如图所示的两个转盘分别被均匀地分成3个和4个扇形,每个扇形上都标有一个实数.同时自由转动两个转盘,转盘停止后(若指针指在分格线上,则重转),两个指针都落在无理数上的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
分析:先把各个数化简,再进一步分析所有等可能到某种效果的可能,然后根据概率公式求出该事件的概率即可.
解答:解:(π,
),(π,
),(π,sin60°),(π,3.14),(2,
),(2,
),
(2,sin60°),(2,3.14),(1,
),(1,
),(1,sin60°),(1,3.14).
可知共有3×4=12种可能,两个指针都落在无理数上的有(π,
)和(π,sin60°)2种,所以两个指针都落在无理数上的概率是
=
.
故选C.
| 5 |
| 22 |
| 7 |
| 5 |
| 22 |
| 7 |
(2,sin60°),(2,3.14),(1,
| 5 |
| 22 |
| 7 |
可知共有3×4=12种可能,两个指针都落在无理数上的有(π,
| 5 |
| 2 |
| 12 |
| 1 |
| 6 |
故选C.
点评:本题考查求随机事件概率的方法.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
 能使游戏对双方公平?
能使游戏对双方公平? 小明和小刚用如图所示的两个转盘做游戏,游戏规则如下:分别旋转两个转盘,当两个转盘所转到的数字之积为奇数时,小明得2分;当所转到的数字之积为偶数时,小刚得1分.这个游戏对双方公平吗?若公平,说明理由.若不公平,如何修改规则才能使游戏对双方公平?
小明和小刚用如图所示的两个转盘做游戏,游戏规则如下:分别旋转两个转盘,当两个转盘所转到的数字之积为奇数时,小明得2分;当所转到的数字之积为偶数时,小刚得1分.这个游戏对双方公平吗?若公平,说明理由.若不公平,如何修改规则才能使游戏对双方公平? 得3分,否则小刚得1分.
得3分,否则小刚得1分.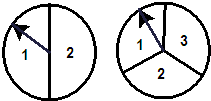 娜相得1分.
娜相得1分.