题目内容
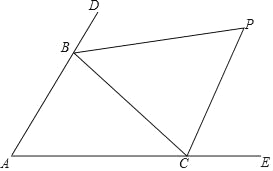
【题目】已知Rt△ABC中,∠B=90°,AC=20,AB=10,P是边AC上一点(不包括端点A、C),过点P作PE⊥BC于点E,过点E作EF∥AC,交AB于点F.设PC=x,
PE=y.
(1)求y与x的函数关系式;
(2)是否存在点P使△PEF是Rt△?若存在,求此时的x的值;若不存在,请说明理由.
【答案】
(1)解:在Rt△ABC中,∠B=90°,AC=20,AB=10,
∴sinC= ![]() ,
,
∵PE⊥BC于点E,
∴sinC= ![]() =
= ![]() ,
,
∵PC=x,PE=y,
∴y= ![]() x(0<x<20)
x(0<x<20)
(2)解:存在点P使△PEF是Rt△,
①如图1,当∠FPE=90°时,四边形PEBF是矩形,BF=PE= ![]() x,
x,
四边形APEF是平行四边形,PE=AF= ![]() x,
x,
∵BF+AF=AB=10,
∴x=10;
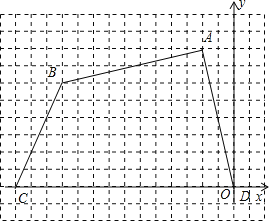
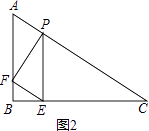
②如图2,当∠PFE=90°时,Rt△APF∽Rt△ABC,
∠ARP=∠C=30°,AF=40﹣2x,
平行四边形AFEP中,AF=PE,即:40﹣2x= ![]() x,
x,
解得x=16;
③当∠PEF=90°时,此时不存在符合条件的Rt△PEF.
综上所述,当x=10或x=16,存在点P使△PEF是Rt△.

【解析】考查了相似三角形的判定与性质,平行四边形的性质,矩形的性质,解直角三角形,注意分类思想的运用,综合性较强,难度中等.(1)在Rt△ABC中,根据三角函数可求y与x的函数关系式;(2)分三种情况:①如图1,当∠FPE=90°时,②如图2,当∠PFE=90°时,③当∠PEF=90°时,进行讨论可求x的值.
【考点精析】通过灵活运用平行四边形的性质和矩形的性质,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;矩形的四个角都是直角,矩形的对角线相等即可以解答此题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案