题目内容
【题目】如图,已知![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上一点(不与端点
上一点(不与端点![]() 重合),
重合),![]() 、
、![]() 分别平分
分别平分![]() 和
和![]() 交
交![]() 于点
于点![]() 、
、![]() .
.
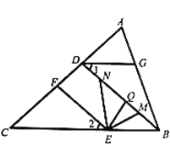
(1)请说明:![]() ;
;
(2)当点![]() 在
在![]() 上移动时,请写出
上移动时,请写出![]() 和
和![]() 之间满足的数量关系为______;
之间满足的数量关系为______;
(3)若![]() ,则当点
,则当点![]() 移动到使得
移动到使得![]() 时,请直接写出
时,请直接写出![]() ______(用含
______(用含![]() 的代数式表示).
的代数式表示).
【答案】(1)见解析;(2)∠BQE=2∠BNE,证明见解析;(3)∠BEQ=![]() ,证明见解析.
,证明见解析.
【解析】
(1)根据![]() ,可证明
,可证明![]() ,从而可证明∠1=∠DBC,根据
,从而可证明∠1=∠DBC,根据![]() 可证明
可证明![]() ,从而证明BD//EF;
,从而证明BD//EF;
(2)通过角平分线和平行线的性质可证明∠BNE=∠NEQ,通过三角形的外角定理可证明∠BQE=2∠BNE;
(3)通过![]() 和三角形内角和定理可证明∠BEM=∠BNE,由(1)中∠BNE=∠NEQ可得∠BEM=∠NEQ,所以∠BEQ=∠MEN,通过角平分线的性质可得∠MEN=
和三角形内角和定理可证明∠BEM=∠BNE,由(1)中∠BNE=∠NEQ可得∠BEM=∠NEQ,所以∠BEQ=∠MEN,通过角平分线的性质可得∠MEN=![]() =
=![]() ,即∠BEQ=
,即∠BEQ=![]() .
.
(1)证明:
![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
∴BD//EF.
(2)∠BQE=2∠BNE,证明如下:
∵BD//EF
∴∠FEN=∠BNE
又∵EN平分∠QEF,
∴∠FEN=∠NEQ,
∴∠BNE=∠NEQ,
∵∠BNE+∠NEQ=∠BQE,
∴∠BQE=2∠BNE.
(3)∠BEQ=![]() ,证明如下:
,证明如下:
∵EN平分∠QEF,
∴∠NEQ=![]() ,
,
同理可得∠QEM=![]() ,
,
∴∠MEN=![]() ,
,
∵![]() ,
,
∴∠2=![]() ,
,
∴∠BEF=180°-![]() ,
,
∴∠MEN=![]() ,
,
在△BEM中,∠CBD+∠BME+∠BEM=180°,
在△BEN中,∠CBD+∠BNE+∠BEN=180°,
∵![]() ,
,
∴∠BEM=∠BNE,
∵由(1)得∠BNE=∠NEQ,
∴∠BEM=∠NEQ,
∴∠BEQ=∠BEM+∠MEQ=∠NEQ+∠MEQ=![]() .
.

练习册系列答案
相关题目



