题目内容
【题目】如图所示,直线![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() ,
,![]() ,与坐标轴交于A、B两点.
,与坐标轴交于A、B两点.
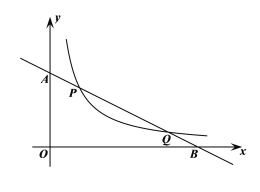
(1)求一次函数与反比例函数的解析式;
(2)观察图象,当![]() 时,直接写出不等式
时,直接写出不等式![]() 的解集;
的解集;
(3)将直线![]() 向下平移
向下平移![]() 个单位,若直线与反比例函数
个单位,若直线与反比例函数![]() 的图象有唯一交点,求
的图象有唯一交点,求![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() 的值为1.
的值为1.
【解析】
(1)把点![]() 代入
代入![]() 求得m=8,从而求出反比例函数解析式,再把P(2,a)代入
求得m=8,从而求出反比例函数解析式,再把P(2,a)代入![]() 求得a=8,最后把P(2,4),Q(8,1)代入
求得a=8,最后把P(2,4),Q(8,1)代入![]() ,求出k和b的值即可;
,求出k和b的值即可;
(2)根据两函数交点坐标结合图象即可得出不等式![]() 的解集;
的解集;
(3)平移后的直线解析式与反比例函数解析式联立方程组,根据两函数图象有唯一交点,得△=0,求解方程即可.
(1)把![]() 代入
代入![]() 得:
得:
![]()
∴反比例函数的解析式为![]() .
.
把![]() 代入
代入![]() 得:
得:
![]()
∴![]()
把![]() ,
,![]() 分别代入
分别代入![]() 得:
得:
![]() ,解之得:
,解之得: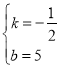
∴一次函数的解析式为![]() ;
;
(2)∵两函数图象的交点为![]() ,
,![]()
观察图象得,当![]() 或
或![]() 时,
时,![]() ;
;
(3)将直线![]() 向下平移
向下平移![]() 个单位后,直线的解析式为
个单位后,直线的解析式为![]()
∵直线![]() 与双曲线
与双曲线![]()
![]() 有唯一交点
有唯一交点
∴方程![]() 有唯一解
有唯一解
整理得:![]()
∴![]()
解之得:![]() (舍去).
(舍去).
∴![]() 的值为1.
的值为1.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
【题目】某水果店计划购进甲、乙两种高档水果共400千克,每千克的售价、成本与购进数量(千克)之间关系如表:
每千克售价(元) | 每千克成本(元) | |
甲 | ﹣0.1x+100 | 50 |
乙 | ﹣0.2x+120(0<x≤200) | 60 |
|
(1)若甲、乙两种水果全部售完,求水果店获得总利润y(元)与购进乙种水果x(千克)之间的函数关系式(其他成本不计);
(2)若购进两种水果都不少于100千克,当两种水果全部售完,水果能获得的最大利润.