Question

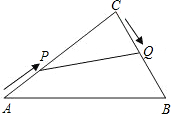在Rt△ABC中，∠C=90°，AC=20cm，BC=15cm．现有动点P从点A出发，沿AC向点C方向运动，动点Q从点C出发，沿线段CB也向点B方向运动．如果点P的速度是4cm/秒，点Q的速度是2cm/秒，它们同时出发，当有一点到达所在线段的端点时，就停止运动，设运动的时间为t秒．
求：（1）用含t的代数式表示Rt△CPQ的面积S；
（2）当t=3秒时，P、Q两点之间的距离是多少？
（3）当t为多少秒时，以点C、P、Q为顶点的三角形与△ABC相似？

Answer 1

分析：（1）由点P，点Q的运动速度和运动时间，又知AC，BC的长，可将CP、CQ用含t的表达式求出，代入直角三角形面积公式S_△CPQ=

1

2

CP×CQ求解；
（2）在Rt△CPQ中，由（1）可知CP、CQ的长，运用勾股定理可将PQ的长求出；
（3）应分两种情况，当Rt△CPQ∽Rt△CAB时，根据

CP

CA

=

CQ

CB

，可将时间t求出；当Rt△CPQ∽Rt△CBA时，根据

CP

CB

=

CQ

CA

，可求出时间t．

解答：解：（1）由题意得AP=4t，CQ=2t，则CP=20-4t，
因此Rt△CPQ的面积为S=

1

2

×(20-4t)×2t=20t-4t2cm²；

（2）当t=3秒时，CP=20-4t=8cm，CQ=2t=6cm，
由勾股定理得PQ=

CP2+CQ2

=

82+62

=10cm；

（3）分两种情况：
①当Rt△CPQ∽Rt△CAB时，

CP

CA

=

CQ

CB

，即

20-4t

20

=

2t

15

，解得t=3秒；
②当Rt△CPQ∽Rt△CBA时，

CP

CB

=

CQ

CA

，即

20-4t

15

=

2t

20

，解得t=

40

11

秒．
因此t=3秒或t=

40

11

秒时，以点C、P、Q为顶点的三角形与△ABC相似．

点评：本题主要考查相似三角形性质的运用，在解第三问时应分两种情况进行求解，在解题过程应防止漏解或错解．