题目内容
【题目】如图1,Rt△ABC≌Rt△DFE,其中∠ACB=∠DFE=90°,BC=EF.
(1)若两个三角形按图2方式放置,AC、DF交于点O,连接AD、BO,则AF与CD的数量关系为 ,BO与AD的位置关系为 ;
(2)若两个三角形按图3方式放置,其中C、B(D)、F在一条直线上,连接AE,M为AE中点,连接FM、CM.探究线段FM与CM之间的关系,并证明;
(3)若两个三角形按图4方式放置,其中B、C(D)、F在一条直线上,点G、H分别为FC、AC的中点,连接GH、BE交于点K,求证:BK=EK.

【答案】(1)AF=CD, BO⊥AD;(2)FM=MC,FM⊥CM,理由见解析;(3)证明见解析.
【解析】
(1)利用全等三角形的性质,线段的垂直平分线的判定定理即可解决问题;
(2)结论:FM=MC,FM⊥CM.如图3中,延长FM交CA的延长线于H.想办法证明△FCH是等腰直角三角形,FM=MH即可解决问题;
(3)如图4中,连接BH,EG,在HG上取一点J,使得BJ=BH.想办法证明△BKJ≌△EKG即可解决问题;
(1)如图2中,
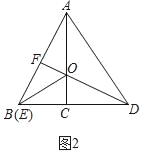
∵Rt△ABC≌Rt△DFE(已知),
∴AB=BD,BC=BF,
∴AF=CD,
∵∠AFO=∠DCO=90°,∠AOF=∠DOC,
∴△AOF≌△DOC(AAS),
∴OA=OC,∵BA=BD,
∴BO垂直平分线段AD.
∴BO⊥AD,
故答案为:AF=CD,BO⊥AD.
(2)结论:FM=MC,FM⊥CM.
理由:如图3中,延长FM交CA的延长线于H.
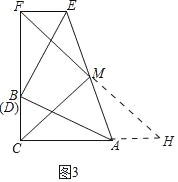
∵∠ACB+∠EFC=180°,B,F,C共线,
∴EF∥CH,
∴∠EFM=∠H,
∵EM=MA,∠EMF=∠AMH,
∴△EFM≌△AHM(AAS),
∴FM=MH,EF=AH,
∵∠FCH=90°,
∴CM=FM=MH,
即FM=MC,
∵△Rt△ABC≌Rt△DFE(已知),
∴BF=AC,EF=BC,
∴BA=AH,
∴FC=CH,
∵FM=MH,
∴CM⊥FM.
(3)如图4中,连接BH,EG,在HG上取一点J,使得BJ=BH.
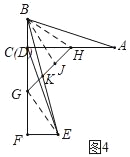
∵Rt△ABC≌Rt△DFE(已知),
∴BC=EF,AC=CF,
∵CH=AH,CG=GF,
∴CH=FG,
∵∠BCH=∠F=90°,
∴△BCH≌△EFG(SAS),
∴∠CBH=∠FEG,
∵CH=CG,∠GCH=90°,
∴∠CGH=∠CHG=45°,
∴∠BHG=180°﹣45°﹣∠GBH=135°﹣∠GBH,
∵∠CGE=∠CGH+∠HGE=90°+∠GEF,
∴∠HGE=45°+∠GEF,
∴∠HGE+∠BHG=180°,
∵∠BJK+∠BJH=180°,∠BJH=∠BHJ,
∴∠BJK=∠HGE,
∵GE=BH=BJ,∠BKJ=∠GKE,
∴△BKJ≌△EKG(AAS),
∴BJ=GE.