题目内容
 如图所示,已知等边△ABC中,BD=CE,AD与BE相交于点P,求∠APE是度数.
如图所示,已知等边△ABC中,BD=CE,AD与BE相交于点P,求∠APE是度数.分析:根据等边三角形的性质证明△ABD≌△BCE就可以得出∠BAD=∠CBE,由∠APE=∠ABP+∠BAP而得出结论.
解答:解:∵△ABC是等边三角形,
∴AB=BC,∠ABC=∠C=60°.
在△ABD和△BCE中
,
∴△ABD≌△BCE(SAS),
∴∠BAD=∠CBE.
∵∠APE=∠ABP+∠BAP,
∴∠APE=∠ABP+∠CBE.
∵∠ABP+∠CBE=∠ABC=60°,
∴∠APE=60°.
答:∠APE=60°.
∴AB=BC,∠ABC=∠C=60°.
在△ABD和△BCE中
|
∴△ABD≌△BCE(SAS),
∴∠BAD=∠CBE.
∵∠APE=∠ABP+∠BAP,
∴∠APE=∠ABP+∠CBE.
∵∠ABP+∠CBE=∠ABC=60°,
∴∠APE=60°.
答:∠APE=60°.
点评:本题考查了等边三角形的性质的运用,全等三角形的判定及性质的运用,三角形外角与内角的关系的运用,解答时证明三角形全等是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


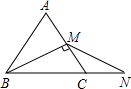 如图所示,已知等边三角形ABC的周长是2a,BM是AC边上的高,N为BC延长线上的一点,且CN=CM,则BN=
如图所示,已知等边三角形ABC的周长是2a,BM是AC边上的高,N为BC延长线上的一点,且CN=CM,则BN=