题目内容
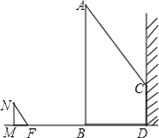
【题目】如图,已知四边形ABCD是矩形,且MO=MD=4,MC=3.
(1)求直线BM的解析式;
(2)求过A、M、B三点的抛物线的解析式;
(3)在(2)中的抛物线上是否存在点P,使△PMB构成以BM为直角边的直角三角形?若没有,请说明理由;若有,则求出一个符合条件的P点的坐标.

【答案】(1)y=-![]() x+4.(2)y=-
x+4.(2)y=-![]() x2-
x2-![]() x+4;(3)见解析(-
x+4;(3)见解析(-![]() )(-
)(-![]() ).
).
【解析】
(1)根据MO=MD=4,MC=3就可以求出A、M、B三点的作坐标,根据待定系数法就可以求出直线BM的解析式与抛物线的解析式.
(2)根据(1)中A、M、B三点的作坐标,根据待定系数法就可以求出抛物线的解析式.
(3)过M、B作MB的垂线,它与抛物线的交点即为P点,因而符合条件的P点是存在的.当∠PMB=90°时,过P作PH⊥DC交于H,则可证△MPH∽△BMC,得到PH:HM=CM:CB=3:4,因而可以设HM=4a(a>0),则PH=3a,则P点的坐标为(-4a,4-3a).将P点的坐标代入y=-![]() x2-
x2-![]() +4就可以求出a的值,进而求出P点的坐标.
+4就可以求出a的值,进而求出P点的坐标.
解:(1)∵MO=MD=4,MC=3,
∴M、A、B的坐标分别为(0,4),(-4,0),(3,0)
设BM的解析式为y=kx+b;
则![]() ,解得:
,解得: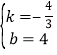
∴BM的解析式为y=![]() x+4.
x+4.
(2)设抛物线的解析式为y=a(x+4)(x-3)
将M(0,4)的坐标代入得a=-![]()
∴y=-![]() (x+4)(x-3)=-
(x+4)(x-3)=-![]() x2-
x2-![]() x+4
x+4
(3)设抛物线上存在点P,使△PMB构成直角三角形.
①过M作MB的垂线与抛物线交于P,过P作PH⊥DC交于H,
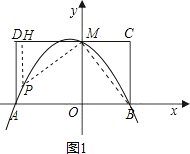
∴∠PMB=90°,
∴∠PMH=∠MBC,
∴△MPH∽△BMC,
∴PH:HM=CM:CB=3:4
设HM=4a(a>0),则PH=3a
∴P点的坐标为(-4a,4-3a)
将P点的坐标代入y=-![]() x2-
x2-![]() x+4得:
x+4得:
4-3a=-![]() (-4a)2-
(-4a)2-![]() ×(-4a)+4
×(-4a)+4
解得a=0(舍出),a=![]() ,
,
∴P点的坐标为(-![]() ,
,![]() )
)
②或者,抛物线上存在点P,使△PMB构成直角三角形.
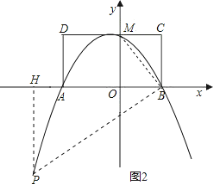
过M作MB的垂线与抛物线交于P,设P的坐标为(x0,y0),
由∠PMB=90°,∠PMD=∠MBC,
过P作PH⊥DC交于H,则MH=-x0,PH=4-y0
∴由tan∠PMD=tan∠MBC
得![]() =
=![]() ,
,
∴![]() =
=![]() +4
+4
∴![]() +4=-
+4=-![]() -
-![]() +4
+4
∴![]() ,
,![]() =0(舍去)
=0(舍去)
∴![]() =
=![]() (
(![]() )+4=
)+4=![]() ,
,
∴P点的坐标为(![]() ,
,![]() )
)
类似的,如果过B作BM的垂线与抛物线交于点P,
设P的坐标为(x0,y0),
同样可求得![]() =
=![]() -
-![]() ,
,
由![]() -
-![]() =-
=-![]() -
-![]() +4
+4
∴![]() ,
,![]() =3(舍去)
=3(舍去)
![]() =
=![]() (
(![]() )-
)-![]() =-
=-![]()
这时P的坐标为(![]() ,-
,-![]() ).
).

 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案