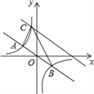
题目内容
【题目】如图,平行四边形ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB丁点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列四个结论:①∠ACD=30°;②![]() ;③
;③![]() =Ac·AD;④OE:OA=1:
=Ac·AD;④OE:OA=1: ![]() 其中结论正确的序号是____.(把所有正确结论的序号都选上)
其中结论正确的序号是____.(把所有正确结论的序号都选上)
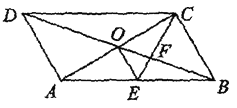
【答案】①③④
【解析】∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=60°,∠BAD=120°,
∵CE平分∠BCD交AB于点E,
∴∠DCE=∠BCE=60°
∴△CBE是等边三角形,
∴BE=BC=CE,
∵AB=2BC,
∴AE=BC=CE,
∴∠ACB=90°,
∴∠ACD=∠CAB=30°,故①正确;
②![]() 不正确,
不正确,
∵AC⊥BC,
∴![]() =Ac·AD,故③正确,
=Ac·AD,故③正确,
在Rt△ACB中,∠ACB=90°,∠CAB=30°,
∴AC=![]() BC,
BC,
∵AO=OC,AE=BE,
∴OE=![]() BC,OA=
BC,OA=![]() BC,
BC,
∴OE:OA= =
=![]() ,
,
故④正确;
答案为:①③④
“点睛”此题考查了相似三角形的判定和性质,平行四边形的性质、三角形中位线的性质以及等边三角形的判定与性质.注意证得△BCE是等边三角形,OE是△ABC的中位线是关键.

练习册系列答案
相关题目