题目内容
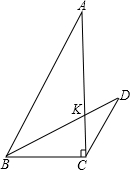在直角三角形ABC中，∠ACB=90°，过点B作线段BD交AC于点K，且CD∥AB，若∠A=36°，∠DBC=25°，则∠D等于
- A.29°
- B.25°
- C.21°
- D.19°
A
分析：利用互余和平行线的性质即可求得．
解答：∵∠ACB=90°，∠A=36°，
∴∠ABC=54°，
∴∠ABD=54°-25°=29°．
∵CD∥AB，
∴∠D=∠ABD=29°．
故答案A．
点评：主要考查了平行线的性质和三角形的内角和是180度．求角的度数常常要用到“三角形的内角和是180°这一隐含的条件．
分析：利用互余和平行线的性质即可求得．
解答：∵∠ACB=90°，∠A=36°，
∴∠ABC=54°，
∴∠ABD=54°-25°=29°．
∵CD∥AB，
∴∠D=∠ABD=29°．
故答案A．
点评：主要考查了平行线的性质和三角形的内角和是180度．求角的度数常常要用到“三角形的内角和是180°这一隐含的条件．
练习册系列答案
相关题目
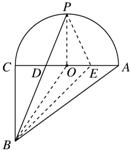6、如图，在直角三角形ABC中，∠ACB=90°，CA=4，点P是半圆弧AC的中点，连接BP，线段即把图形APCB（指半圆和三角形ABC组成的图形）分成两部分，则这两部分面积之差的绝对值是
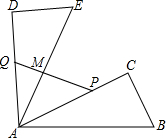使点B落在点E处，点C落在点D处．P、Q分别为线段AC、AD上的两个动点，且AQ=2PC，连接PQ交线段AE于点M．
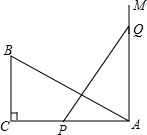如图，在直角三角形ABC中，∠C=90°，AC=20，BC=10，PQ=AB，P，Q两点分别在线段AC和过点A且垂直于AC的射线AM上运动，且点P不与点A，C重合，那么当点P运动到什么位置时，才能使△ABC与△APQ全等？