��Ŀ����
��ͼ����ֱ��������ABC�У���C=90�㣬��A=30�㣬AC=4������ABC�Ƶ�A��ʱ����ת60�㣬 ʹ��B���ڵ�E������C���ڵ�D����P��Q�ֱ�Ϊ�߶�AC��AD�ϵ��������㣬��AQ=2PC������PQ���߶�AE�ڵ�M��
ʹ��B���ڵ�E������C���ڵ�D����P��Q�ֱ�Ϊ�߶�AC��AD�ϵ��������㣬��AQ=2PC������PQ���߶�AE�ڵ�M����1����AQ=x����APQ���Ϊy����y����x�ĺ�����ϵʽ����д�����Ķ�����
��2�����Ե�PΪԲ�ģ�PCΪ�뾶��Բ���AB���У���AQ�ij���
��3���Ƿ���ڵ�Q��ʹ�á�AQM����APQ�͡�APM��������������һ�����������������ƣ������������AQ�ij�������������˵�����ɣ�
��������1����AQ=x����������x��ʾ��AP�ij���Ȼ����ݡ�APQ�����=
AQ•AP•sin��QAP��������⣻
��2������P��PF��AB������ΪF����PC=PF��ֱ��������APF�и��ݱ߽ǹ�ϵ������⣻
��3����AQM����APQ�͡�APM���������������������������ƣ����ɷֳ�3������������ۣ��ٸ���sin��QPA=
�����ɵõ�����AQ�ķ��̣��Ӷ���⣮
| 1 |
| 2 |
��2������P��PF��AB������ΪF����PC=PF��ֱ��������APF�и��ݱ߽ǹ�ϵ������⣻
��3����AQM����APQ�͡�APM���������������������������ƣ����ɷֳ�3������������ۣ��ٸ���sin��QPA=
| PF |
| AP |
���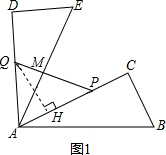 �⣺��1����ͼ1����Q��QH��AC������ΪH����1�֣�
�⣺��1����ͼ1����Q��QH��AC������ΪH����1�֣�
�ߡ�ABC�Ƶ�A��ʱ����ת60�㣬
���DAC=60�㣬��ABC�ա�ADE��
���DAE=��BAC=30�㣬��EAC=30�㣬
����ֱ��������AQH��sin60��=
��
��QH=
x����1�֣�
��AQ=2PC��AC=4��
��PC=
xAP=4-
x����1�֣�
��S��AQP=
AP•QH��
��y=
��4-x��•
x=-
x2+
x��0��x��4����
��2����ͼ2����P��PF��AB������ΪF����1�֣�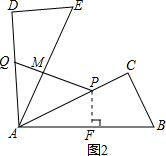
���Ե�PΪԲ�ģ�PCΪ�뾶��Բ���AB���У�
��PC=P��F��1�֣�
��ֱ��������APF�У�sin30��=
��
��
=
��
��x=
����2�֣�
�������Ե�PΪԲ�ģ�PCΪ�뾶��Բ���AB���У���AQ�ij�Ϊ
��
��3��������ڵ�Q��ʹ�á�AQM����APQ�͡�APM��������������һ�����������������ƣ�
����ͼ3������AQM���APQ����ʱ��
�ߡ�AQM=��PQA����QAM�١�QAP��
���QAM=��QPA=30�㣬
���PQA=90�㣬
��sin��QPA=
=
��
��x=
����2�֣�
�ڵ���APQ���APM����ʱ��
�ߡ�APQ=��APM����QAM�١�QAP��
���PAM=��PQA=30�㣬
���QPA=90�㣬
��sin��PQA=
=
��
��x=4����2�֣�
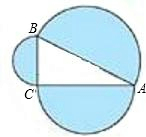
����ͼ4������AQM���APM����ʱ��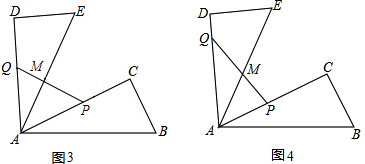
�ߡ�QAM=��PAM=30�㣬��AQM�١�AMP��
���AQM=��APM��
��AQ=AP��
��x=4-
x��
��x=
����1�֣�
�൱AQΪ
��4��
ʱ����AQM����APQ�͡�APM��������������һ�����������������ƣ�
 �⣺��1����ͼ1����Q��QH��AC������ΪH����1�֣�
�⣺��1����ͼ1����Q��QH��AC������ΪH����1�֣��ߡ�ABC�Ƶ�A��ʱ����ת60�㣬
���DAC=60�㣬��ABC�ա�ADE��
���DAE=��BAC=30�㣬��EAC=30�㣬
����ֱ��������AQH��sin60��=
| QH |
| AQ |
��QH=
| ||
| 2 |
��AQ=2PC��AC=4��
��PC=
| 1 |
| 2 |
| 1 |
| 2 |
��S��AQP=
| 1 |
| 2 |
��y=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 8 |
| 3 |
��2����ͼ2����P��PF��AB������ΪF����1�֣�

���Ե�PΪԲ�ģ�PCΪ�뾶��Բ���AB���У�
��PC=P��F��1�֣�
��ֱ��������APF�У�sin30��=
| PF |
| AP |
��
| 1 |
| 2 |
| ||
4-
|
��x=
| 8 |
| 3 |
�������Ե�PΪԲ�ģ�PCΪ�뾶��Բ���AB���У���AQ�ij�Ϊ
| 8 |
| 3 |
��3��������ڵ�Q��ʹ�á�AQM����APQ�͡�APM��������������һ�����������������ƣ�
����ͼ3������AQM���APQ����ʱ��
�ߡ�AQM=��PQA����QAM�١�QAP��
���QAM=��QPA=30�㣬
���PQA=90�㣬
��sin��QPA=
| AQ |
| AP |
| 1 |
| 2 |
| x | ||
4-
|
��x=
| 8 |
| 5 |
�ڵ���APQ���APM����ʱ��
�ߡ�APQ=��APM����QAM�١�QAP��
���PAM=��PQA=30�㣬
���QPA=90�㣬
��sin��PQA=
| AP |
| AQ |
| 1 |
| 2 |
4-
| ||
| x |
��x=4����2�֣�
����ͼ4������AQM���APM����ʱ��

�ߡ�QAM=��PAM=30�㣬��AQM�١�AMP��
���AQM=��APM��
��AQ=AP��
��x=4-
| 1 |
| 2 |
��x=
| 8 |
| 3 |
�൱AQΪ
| 8 |
| 5 |
| 8 |
| 3 |
������������Ҫ��������ת�����ʣ��Լ����������ε��ж������ʣ���ȷ�������ۣ�����sin��QPA=
��һ��ϵ�ǽ���Ĺؼ���
| PF |
| AP |

��ϰ��ϵ�д�
�����Ŀ
 ��ͼ����ֱ��������ABC�У���C=90�㣬AB=4����Ӱ���ֵ����Ϊ��������
��ͼ����ֱ��������ABC�У���C=90�㣬AB=4����Ӱ���ֵ����Ϊ��������| A��2�� | B��3�� | C��4�� | D��6�� |
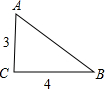
 ��ͼ����ֱ���������У�һֱ�DZ߱���һֱ�DZ߳�1����б�߳�Ϊ5��
��ͼ����ֱ���������У�һֱ�DZ߱���һֱ�DZ߳�1����б�߳�Ϊ5�� ��ͼ����ֱ��������ABC�У�ADΪб���ϵĴ��ߣ�AEΪ��ƽ���ߣ�AFΪ���ߣ�
��ͼ����ֱ��������ABC�У�ADΪб���ϵĴ��ߣ�AEΪ��ƽ���ߣ�AFΪ���ߣ� 9����ͼ����ֱ��������ABC�У���C=90�㣬AC=10cm��BC=5cm��һ���߶�PQ=AB��P��Q����ֱ���AC��AC�Ĵ���AX���ƶ�����AP=
9����ͼ����ֱ��������ABC�У���C=90�㣬AC=10cm��BC=5cm��һ���߶�PQ=AB��P��Q����ֱ���AC��AC�Ĵ���AX���ƶ�����AP=