题目内容
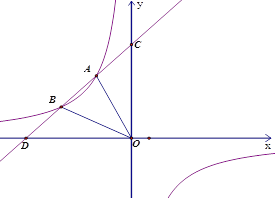
【题目】如图，一次函数
与反比例函数
的图象相交于A，B两点，且与坐标轴的交点为（﹣6，0），（0，6），点B的横坐标为﹣4．点A的纵坐标为4.
（1）试确定反比例函数的解析式；
（2）求△AOB的面积；
（3）直接写出不等式
的解集．
【答案】(1) 
；(2) 6；(3) -4＜x＜-2或x>0
【解析】分析：（1）根据待定系数法就可以求出函数的解析式；
（2）求△AOB的面积就是求A，B两点的坐标，将一次函数与反比例函数的解析式组成方程即可求得；
（3）观察图象即可求得一次函数比反比例函数大的区间．
详解：（1）设一次函数解析式为y=kx+b，
∵一次函数与坐标轴的交点为（-6，0），（0，6），
∴
解得： 
，
∴一次函数关系式为：y=x+6，
∴B（-4，2），
∴反比例函数关系式为： 
；
（2）∵点A与点B是反比例函数与一次函数的交点，
∴A（-2，4），
∴S△AOB=6×6÷2-6×2=6；
（3）-4＜x＜-2或x>0．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
【题目】自行车厂某周计划生产2100辆电动车，平均每天生产电动车300辆．由于各种原因，实际每天的生产量与计划每天的生产量相比有出入，下表是该周的实际生产情况（超产记为正、减产记为负，单位：辆）：
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
减增 |
|
|
|
|
|
|
|
（1）该厂星期一生产电动车________辆；
(2)生产量最多的一天比生产量最少的一天多生产电动车________辆；
(3)该厂实行记件工资制，每生产一辆车可得60元，那么该厂工人这一周的工资总额是多少元？
