题目内容
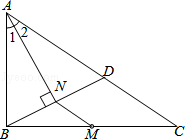
如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3
(1)求证:BN=DN;
(2)求△ABC的周长.

(1)求证:BN=DN;
(2)求△ABC的周长.
解:(1)证明:在△ABN和△ADN中,∵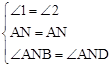 ,
,
∴△ABN≌△ADN(ASA)。
∴BN=DN。
(2)∵△ABN≌△ADN,∴AD=AB=10,DN=NB。
又∵点M是BC中点,∴MN是△BDC的中位线。
∴CD=2MN=6。
∴△ABC的周长=AB+BC+CD+AD=10+15+6+10=41。
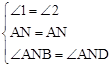 ,
,∴△ABN≌△ADN(ASA)。
∴BN=DN。
(2)∵△ABN≌△ADN,∴AD=AB=10,DN=NB。
又∵点M是BC中点,∴MN是△BDC的中位线。
∴CD=2MN=6。
∴△ABC的周长=AB+BC+CD+AD=10+15+6+10=41。
(1)证明△ABN≌△ADN,即可得出结论。
(2)先判断MN是△BDC的中位线,从而得出CD,由(1)可得AD=AB=10,从而计算周长即可。
(2)先判断MN是△BDC的中位线,从而得出CD,由(1)可得AD=AB=10,从而计算周长即可。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

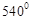 ,则这个多边形是【 】
,则这个多边形是【 】