题目内容
 如图,D为等边△ABC的BC边上一点,已知BD=1,CD=2,CH⊥AD于点H,连接BH.试证:∠BHD=60°.
如图,D为等边△ABC的BC边上一点,已知BD=1,CD=2,CH⊥AD于点H,连接BH.试证:∠BHD=60°.
 解:作AE⊥DC于E,
解:作AE⊥DC于E,∵CH⊥AD,
∴∠DHC=∠AED=90°,
∵∠ADE=∠CDH,
∴△DAE∽△DCH,
∵等边△ABC中,BD=1,CD=2,
∴BE=
 BC=
BC= ×(2+1)=1.5,
×(2+1)=1.5,∴DE=BE-BD=0.5,
∵
 ,
,∴DH×DA=DE×DC=0.5×2=1=BD2,
∴
 ,
,∵∠BDH=∠ADB,
∴△BDH∽△ADB,
∴∠BHD=∠ABC=60°.
分析:首先作AE⊥DC于E,然后证得△DAE∽△DCH,又由三线合一的性质求得DE的长,即可得DH×DA=DE×DC=1=BD2,则可证得:△BDH∽△ADB,则问题得解.
点评:此题考查了相似三角形的判定与性质.解题的关键是注意数形结合思想的应用.

练习册系列答案
相关题目
 3、如图,△ABC为等边三角形,∠ABC、∠ACB的平分线相交于点O,OE∥AB交BC于点E,OF∥AC交BC于点F,图中等腰三角形共有( )
3、如图,△ABC为等边三角形,∠ABC、∠ACB的平分线相交于点O,OE∥AB交BC于点E,OF∥AC交BC于点F,图中等腰三角形共有( ) 如图,△ABC为等边三角形,点D,E,F分别在AB,BC,CA边上,且△DEF是等边三角形,求证:△ADF≌△CFE.
如图,△ABC为等边三角形,点D,E,F分别在AB,BC,CA边上,且△DEF是等边三角形,求证:△ADF≌△CFE.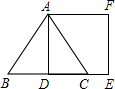 如图,△ABC为等边三角形,AD为BC边上的高,且AB=2,则正方形ADEF的面积为
如图,△ABC为等边三角形,AD为BC边上的高,且AB=2,则正方形ADEF的面积为 (2013•普陀区模拟)如图,△AOB为等边三角形,点B的坐标为(-2,0),过点C(2,0)作直线l交AO于点D,交AB于E,点E在反比例函数
(2013•普陀区模拟)如图,△AOB为等边三角形,点B的坐标为(-2,0),过点C(2,0)作直线l交AO于点D,交AB于E,点E在反比例函数 如图,△AOB为等边三角形,点B的坐标为(-2,0),过点C(2,0)作直线l交AO于D,交AB于E,点E在某反比例函数图象上,当△ADE和△DCO的面积相等时,那么该反比例函数解析式为( )
如图,△AOB为等边三角形,点B的坐标为(-2,0),过点C(2,0)作直线l交AO于D,交AB于E,点E在某反比例函数图象上,当△ADE和△DCO的面积相等时,那么该反比例函数解析式为( )