题目内容
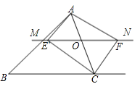
【题目】如图,在△ABC中,AB=AC,∠A=36°,BD,CE是角平分线,则图中的等腰三角形共有

A. 8个 B. 7个 C. 6个 D. 5个
【答案】A
【解析】
根据三角形内角和定理求出∠ABC=∠ACB=72°,根据角平分线求出∠ABD=∠DBC=∠ACE=∠ECB=36°,根据三角形内角和定理求出∠BDC、∠BEC、∠EOB、∠DOC,根据等腰三角形的判定推出即可.
∵AB=AC,∠A=36°,
∴∠ABC=∠ACB=![]() (180°∠A)=72°,
(180°∠A)=72°,
∵BD,CE是角平分线,
∴∠ABD=∠DBC=![]() ∠ABC=36°,∠ACE=∠ECB=36°,
∠ABC=36°,∠ACE=∠ECB=36°,
∴∠A=∠ABD=∠ACE,∠DBC=∠ECB,
∴∠BDC=180°∠ACB∠DBC=180°72°36°=72°,
同理∠BEC=72°,
∴∠BDC=∠ACB,∠BEC=∠EBC,
∴∠EOB=180°∠BEC∠EBD=180°72°36°=72°,
同理∠DOC=72°,
∴∠BEO=∠BOE,∠CDO=∠COD,
即等腰三角形有△OBC,△ADB,△AEC,△BEC,△BDC,△ABC,△EBO,△DCO,共8个,
故选:A.

练习册系列答案
相关题目