Question

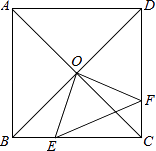
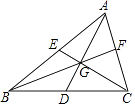
【题目】如图，正方形ABCD中，P是对角线BD上一点，连接AP、，BF⊥AP于H，CP、BH延长线分别交AD边于点E、F。

（1）求证：∠DAP=∠DCE

（2）求证：AE=FD

（3）猜想∠APE与∠FBD的数量关系，并说明理由.

Answer 1

【答案】(1)见解析；（2）见解析；（3），理由见解析

【解析】

（1）证明△ADP≌△CDP，根据全等三角形的对应角相等即可得∠DAP=∠DCE；

（2）证明ΔABF≌ΔDCE，根据全等三角形的对应边相等可得AF=DE，继而可证得答案；

（3）猜想：∠APE=2∠FBD，连接AC，由△ADP≌△CDP，可得AP=CP，继而可推导得出∠APE=2∠ACP，然后再证明∠FBD=∠ECA即可得到.

（1）∵四边形ABCD是正方形，

∴AD=CD，∠ADP=∠CDP，

在△ADP和△CDP中，

，

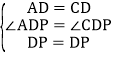∴△ADP≌△CDP，

∴∠DAP=∠DCE；

（2）∵四边形ABCD是正方形，

∴∠BAD=∠ADC=90°，AB=DC，

∴∠ABF+∠AFB=90°，

∵AP⊥BF，

∴∠AHF=90°，

∴∠HAF+ ∠AFB=90°，

∴∠ABF= ∠HAF，

∵∠DAP= ∠DCE，

∴∠ABF=∠DCE，

在ΔABF和ΔDCE中

，

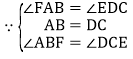∴ΔABF≌ΔDCE，

∴AF=DE，

∴AF+EF=DE+EF，

即AE=FD；

（3）猜想：∠APE=2∠FBD，理由如下：

连接AC，

由（1）知：△ADP≌△CDP，

∴AP=CP，

∴∠PAC=∠PCA，

∴∠APE=2∠ACP，

∵四边形ABCD是正方形，

∴∠ABD=∠DCA=45°，

∴∠ABD－∠ABF=∠DCA－∠DCE，

即∠FBD=∠ECA，

∴∠APE=2∠FBD.