题目内容
【题目】如图1,在四边形ABCD中,如果对角线AC和BD相交并且相等,那么我们把这样的四边形称为等角线四边形.

(1)在“平行四边形、矩形、菱形,正方形”中, 一定是等角线四边形(填写图形名称);
(2)若M、N、P、Q分别是等角线四边形ABCD四边AB、BC、CD、DA的中点,当对角线AC、BD还要满足 时,四边形MNPQ是正方形;
(3)如图2,已知△ABC中,∠ABC=90°,AB=4,BC=3,D为平面内一点.若四边形ABCD是等角线四边形,且AD=BD,求四边形ABCD的面积.
【答案】(1)矩形和正方形;(2)AC⊥BD;(3)3+2![]() .
.
【解析】
(1)只有矩形和正方形的对角线相等,所以矩形和正方形是等角线四边形;
(2)当AC⊥BD时,四边形MNPQ是正方形,首先证明四边形MNPQ是菱形,再证明有一个角是直角即可;
(3)如图2中,作DE⊥AB于E.根据S四边形ABCD=S△ADE+S梯形DEBC计算,求出相关线段即可.
(1)在“平行四边形、矩形、菱形、正方形”中,
∵矩形和正方形的对角线相等,
∴矩形和正方形一定是等角线四边形,
故答案为矩形和正方形.
(2)当AC⊥BD时,四边形MNPQ是正方形.
理由:如图中,

∵M、N、P、Q分别是等角线四边形ABCD四边AB、BC、CD、DA的中点,
∴PQ=MN=![]() AC,PN=QM=
AC,PN=QM=![]() BD,PQ∥AC,MQ∥BD,
BD,PQ∥AC,MQ∥BD,
∵AC=BD,
∴MN=NP=PQ=QM,
∴四边形MNPQ是菱形,
∵∠1=∠2,∠2=∠3,∠1=90°,
∴∠3=90°,
∴四边形NMPQ是正方形.
故答案为AC⊥BD.
(3)如图2中,作DE⊥AB于E.
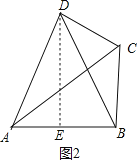
在Rt△ABC中,∵∠ABC=90°,AB=4,BC=3,
∴AC=![]() =5,
=5,
∵AD=BD,DE⊥AB,
∴AE=BE=2,
∵四边形ABCD是等角线四边形,
∴BD=AC=AD=5,
在Rt△BDE中,DE=![]() =
=![]() ,
,
∴S四边形ABCD=S△ADE+S梯形DEBC
=![]() AEDE+
AEDE+![]() (DE+BC)BE
(DE+BC)BE
=![]() ×2×
×2×![]() +
+![]() (
(![]() +3)×2
+3)×2
=3+2![]() .
.
故答案为3+2![]() .
.

【题目】已知A、B两个蔬菜市场各有蔬菜14吨,现要全部运往甲、乙两地,其中甲地需要蔬菜15吨,乙地需要蔬菜13吨,从蔬菜市场A到甲地运费50元/吨,到乙地30元/吨;从蔬菜市场B到甲地运费60元/吨,到乙地45元/吨。
(1)设从蔬菜市场A向甲地运送蔬菜x吨,请完成下表:
运往甲地(单位:吨) | 运往乙地(单位:吨) | |
蔬菜市场A | x | |
蔬菜市场B |
(2)若总运费为1300元,则从蔬菜市场A向甲地运送蔬菜多少吨?