题目内容
【题目】如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒.

(1)当t=1s时,求△ACP的面积.
(2)t为何值时,线段AP是∠CAB的平分线?
(3)请利用备用图2继续探索:当△ACP是等腰三角形时,求t的值.
【答案】(1)6;(2)![]() ;(3)3s或6s或
;(3)3s或6s或![]() s或5.4s.
s或5.4s.
【解析】
(1)当t=1s时,△ACP是直角三角形,根据公式求△ACP的面积;
(2)如图3,过P作PH⊥AB于H,Rt△PHB中,PB=8﹣2t,根据勾股定理列方程可求解;
(3)分四种情况进行讨论:①如图4,根据AC=CP列式求解;②如图5,根据AC=AP列式求解;③如图6,AP=PC,根据AP=PB列式求解;④如图7,AC=CP,根据AP的值列式求解.
解:(1)如图1,点P在BC上,

由题意得:CP=2t,
当t=1时,PC=2,
∴S△ACP=![]() ACPC=
ACPC=![]() ×6×2=6;
×6×2=6;
(2)如图2,

Rt△ACB中,由勾股定理得:AB=![]() =10,
=10,
如图3,AP平分∠CAB,
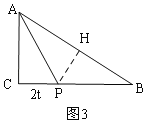
过P作PH⊥AB于H,
∵∠C=90°,
∴PC=PH=2t,
∵∠C=∠AHP=90°,AP=AP,
∴△ACP≌△AHP,
∴AH=AC=6,
∴BH=4,
在Rt△PHB中,PB=8﹣2t,
∴(2t)2+42=(8﹣2t)2,
t=![]() ;
;
则当t=![]() 时,线段AP是∠CAB的平分线;
时,线段AP是∠CAB的平分线;
(3)当△ACP是等腰三角形时,有四种情况:
①如图4,AC=CP时,

由题意得
2t=6,
∴t=3;
②如图5,AC=AP时,
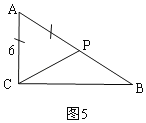
由题意得
18﹣2t=6,
∴t=6;
③如图6,AP=PC时,

过P作PG⊥AC于G,
∵∠C=90°,
∴PG∥BC,
∴AP=PB,
即18﹣2t=2t﹣8,
∴t=![]() ;
;
④如图7,AC=CP时,

过C作CM⊥AB于M,
∴AM=PM=![]() (18-2t)=9-t,
(18-2t)=9-t,
∵![]() AB×CM=
AB×CM=![]() AC×BC,
AC×BC,
∴CM=4.8,
∴AM=![]() =3.6,
=3.6,
∴9-t=3.6,
∴t=5.4,
综上所述,当△ACP是等腰三角形时,t的值是3s或6s或![]() s或5.4s.
s或5.4s.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案



