Question

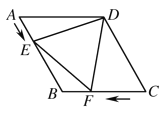
【题目】如图，直角梯形OABC的直角顶点是坐标原点，边OA，OC分别在x轴，y轴的正半轴上．OA∥BC，D是BC上一点，BD=OA=，AB=3，∠OAB=45°，E，F分别是线段OA，AB上的两个动点，且始终保持∠DEF=45°．设OE=x，AF=y，则y与x的函数关系式为_____．

Answer 1

【答案】

【解析】

首先过B作x轴的垂线，设垂足为M，由已知易求得OA=4，在Rt△ABM中，已知∠OAB的度数及AB的长，即可求出AM、BM的长，进而可得到BC、CD的长，再连接OD，证△ODE∽△AEF，通过得到的比例线段，即可得出y与x的函数关系式．

解：过B作BM⊥x轴于M．

在Rt△ABM中，

∵AB=3，∠BAM=45°，

∴AM=BM=，

∵BD=OA= ，

，

∴BC=OA﹣AM=4﹣，CD=BC﹣BD=，

∴D(，)，

．

连接OD，则点D在∠COA的平分线上，所以∠DOE=∠COD=45°．

又∵在梯形DOAB中，∠BAO=45°，

∴由三角形外角定理得：∠ODE=∠DEA﹣45°，又∠AEF=∠DEA﹣45°，

∴∠ODE

=∠AEF，

∴△ODE∽△AEF，

即

∴y与x的解析式为：．

故答案为：．