题目内容
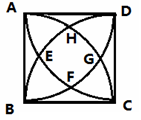
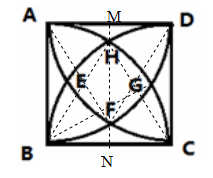
如图,这是当初中央电视台设计台徽时的模型,它是以正方形ABCD的每个顶点为圆心,每边长为半径画圆弧交于E、F、G、H、若边长AB=4cm,则点F到BC的距离是 围成的曲边四边形EFGH的周长是 .

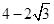 ;
;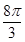 .
.试题分析:连接AF,BH,DF,HC.∵AB=4,AB=BC=BH=CH,∴△BHC是等边三角形,∴边BC上的高线为:
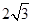 ,同理:AD边上的高线为:
,同理:AD边上的高线为: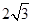 ,延长HF交BC于N,并反向延长HF交AD于M.∵四边形ABCD是正方形,∴AB∥DC,∴MN⊥AD,MN⊥BC,设HF到BC到距离为x,HF到DC的距离为x′,HF=y,由题意可知:x=x′,则
,延长HF交BC于N,并反向延长HF交AD于M.∵四边形ABCD是正方形,∴AB∥DC,∴MN⊥AD,MN⊥BC,设HF到BC到距离为x,HF到DC的距离为x′,HF=y,由题意可知:x=x′,则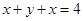 ,∵
,∵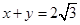 ,∴
,∴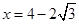 ,∴FN=
,∴FN=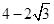 .
.∵△BHC为等边三角形,∴∠HBC=60°,∴∠ABH=30°,同理∠HBG=∠GBC=30°,∴弧AH=弧HG=弧GC,同理可求得:弧EH=弧EF=弧FG=弧HG,∴曲边四边形EFGH的周长是=弧AH的长度的4倍=
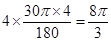 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 .
.
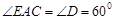 .
.
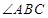 的度数;
的度数;





