题目内容
【题目】如图,已知点O是△ABC的两条角平分线的交点,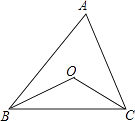
(1)若∠A=30°,则∠BOC的大小是;
(2)若∠A=60°,则∠BOC的大小是;
(3)若∠A=n°,则∠BOC的大小是多少?试用学过的知识说明理由.
【答案】
(1)105°
(2)120°
(3)解:∵如图,在△ABC中,∠A+∠ABC+∠ACB=180°,
在△BOC中,∠BOC+∠OBC+∠OCB=180°,
∵BO,CO分别是∠ABC和∠ACB的平分线,
∴∠ABC=2∠OBC,∠ACB=2∠OCB,
∴∠BOC+ ![]() ∠ABC+
∠ABC+ ![]() ∠ACB=180°,
∠ACB=180°,
又∵在△ABC中,∠A+∠ABC+∠ACB=180°,
∴∠BOC= ![]() ∠A+90°=105°;
∠A+90°=105°;
∴若∠A=n°,∠BOC= ![]() n°+90°;
n°+90°;
【解析】解:(1)∵如图,在△ABC中,∠A+∠ABC+∠ACB=180°,
在△BOC中,∠BOC+∠OBC+∠OCB=180°,
∵BO,CO分别是∠ABC和∠ACB的平分线,
∴∠ABC=2∠OBC,∠ACB=2∠OCB,
∴∠BOC+ ![]() ∠ABC+
∠ABC+ ![]() ∠ACB=180°,
∠ACB=180°,
又∵在△ABC中,∠A+∠ABC+∠ACB=180°,
∴∠BOC= ![]() ∠A+90°=105°;(2)∵如图,在△ABC中,∠A+∠ABC+∠ACB=180°,
∠A+90°=105°;(2)∵如图,在△ABC中,∠A+∠ABC+∠ACB=180°,
在△BOC中,∠BOC+∠OBC+∠OCB=180°,
∵BO,CO分别是∠ABC和∠ACB的平分线,
∴∠ABC=2∠OBC,∠ACB=2∠OCB,
∴∠BOC+ ![]() ∠ABC+
∠ABC+ ![]() ∠ACB=180°,
∠ACB=180°,
又∵在△ABC中,∠A+∠ABC+∠ACB=180°,
∴∠BOC= ![]() ∠A+90°=120°;
∠A+90°=120°;
故答案为:105°,120°.
根据得到∠BOC+∠OBC+∠OCB=180°,根据角平分线的定义得到∠ABC=2∠OBC,∠ACB=2∠OCB,等量代换得到∠BOC+![]() ∠ABC+
∠ABC+![]() ∠ACB=180°,根据三角形的内角和即可得到结论;
∠ACB=180°,根据三角形的内角和即可得到结论;
(2)根据得到∠BOC+∠OBC+∠OCB=180°,根据角平分线的定义得到∠ABC=2∠OBC,∠ACB=2∠OCB,等量代换得到∠BOC+![]() ∠ABC+
∠ABC+![]() ∠ACB=180°,根据三角形的内角和即可得到结论;
∠ACB=180°,根据三角形的内角和即可得到结论;
(3)根据得到∠BOC+∠OBC+∠OCB=180°,根据角平分线的定义得到∠ABC=2∠OBC,∠ACB=2∠OCB,等量代换得到∠BOC+![]() ∠ABC+
∠ABC+![]() ∠ACB=180°,根据三角形的内角和即可得到结论;
∠ACB=180°,根据三角形的内角和即可得到结论;

【题目】某商场销售A,B两种品牌的教学设备,这两种教学设备的进价和售价如表所示:
A | B | |
进价(万元/套) | 1.5 | 1.2 |
售价(万元/套) | 1.65 | 1.4 |
该商场计划购进两种教学设备若干套,共需66万元,全部销售后可获毛利润9万元.[毛利润=(售价﹣进价)×销售量]
(1)该商场计划购进A,B两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少的数量的1.5倍.若用于购进这两种教学设备的总资金不超过69万元,问A种设备购进数量至多减少多少套?