Question

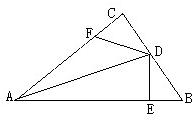19、已知：如图，在△ABC中，∠C=90°，AD平分∠BAC，DE⊥AB于点E，点F在AC上，BD=DF．
（1）求证△CDF≌△EDB；
（2）请你判断BE+DE与DF的大小关系，并证明你的结论．

Answer 1

分析：（1）因为∠C=90°，DE⊥AB，所以∠C=∠DEB，又因为AD平分∠BAC，所以CD=DE，已知BD=DF，则可根据HL判定△CDF≌△EDB；
（2）因为CF=EB，所以BE+DC＞DF．

解答：解：（1）证明：∵DE⊥AB，CD⊥AC，
∴∠C=∠DEB．
∵AD是∠BAC的平分线，
∴CD=DE．
∵BD=DF，
∴△CDF≌△EDB（HL）．

（2）BE+DE＞DF．
∵△CDF≌△EDB，
∴CF=EB．
∴BE+DC＞DF（三角形的两边之和大于第三边）．

点评：本题考查了全等三角形的判定和性质；此题把全等三角形的判定和性质结合求解，有利于培养学生综合运用数学知识的能力．