Question

【题目】如图，在中， ，将绕顶点逆时针旋转得到Rt△DEC,点M是BC的中点，点P是DE的中点，连接PM，若BC =2,∠BAC=30°，则线段PM的最大值是 （ ）

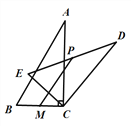
A. 4 B. 3 C. 2 D. 1

Answer 1

【答案】B

【解析】分析：连接CP，由题意可知BC的长，从而求出AB、CM的长，由旋转的性质得出ED的长,再根据直角三角形斜边上的中线是斜边的一半可求出PC的长，最后由三角形的两边之和大于第三边可知，当点P、M、C共线时，PM取最大值.

详解：如图：连接CP，

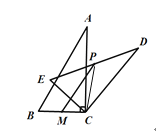
∵∠ACB=90°，∠A=30°，BC=2，

∴AB=2BC=4.

∵BC的中点为M，

∴CM=BC=×2=1.

∵绕点C逆时针旋转任意一个角度得到Rt△DEC，P是Rt△DEC中ED的中点.

∴AB=ED,

∴CP=ED=AB=×4=2.

由三角形的三边关系得，CM+CP＞PM，

∴P、C、M三点共线时PM有最大值.

此时PM=CM+CP=1+2=3．