题目内容
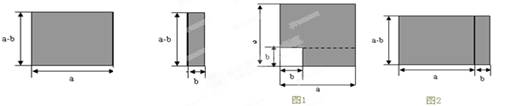
如图所示的两个长方形用不同形式拼成图1和图2两个图形.
(1)若图1中的阴影部分面积为a2-b2;则图2中的阴影部分面积为
(2)由(1)你可以得到等式
(3)根据你所得到的等式解决下面的问题:
①计算:67.752-32.252
②解方程:(x+1)2-(x-1)2=-4.

(1)若图1中的阴影部分面积为a2-b2;则图2中的阴影部分面积为
(a+b)(a-b)
(a+b)(a-b)
.(用含字母a、b的代数式表示)(2)由(1)你可以得到等式
a2-b2=(a+b)(a-b)
a2-b2=(a+b)(a-b)
;(3)根据你所得到的等式解决下面的问题:
①计算:67.752-32.252
②解方程:(x+1)2-(x-1)2=-4.

分析:(1)根据长方形的面积公式列式计算即可得解;
(2)根据两阴影部分的面积相等解答;
(3)分别利用平方差公式进行计算即可得解.
(2)根据两阴影部分的面积相等解答;
(3)分别利用平方差公式进行计算即可得解.
解答:解:(1)图2中的阴影部分面积为(a+b)(a-b);
(2)a2-b2=(a+b)(a-b);
(3)①67.752-32.252
=(67.75+32.25)(67.75-32.25)
=100×35.5
=3550;
②(x+1)2-(x-1)2=-4,
(x+1+x-1)(x+1-x+1)=-4,
4x=-4,
x=-1.
(2)a2-b2=(a+b)(a-b);
(3)①67.752-32.252
=(67.75+32.25)(67.75-32.25)
=100×35.5
=3550;
②(x+1)2-(x-1)2=-4,
(x+1+x-1)(x+1-x+1)=-4,
4x=-4,
x=-1.
点评:本题考查了平方差公式的几何背景,用不同的方法表示出阴影部分的面积是解题的关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
 如图所示,两个长方形重叠部分的面积相当于大长方形面积的六分之一,相当于小长方形面积的四分之一,阴影部分的面积为224cm2,求重叠部分面积.
如图所示,两个长方形重叠部分的面积相当于大长方形面积的六分之一,相当于小长方形面积的四分之一,阴影部分的面积为224cm2,求重叠部分面积.