题目内容
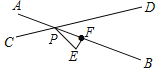
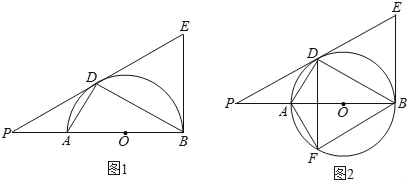
【题目】如图,AB是圆O的直径,O为圆心,AD、BD是半圆的弦,且∠PDA=∠PBD.延长PD交圆的切线BE于点E
(1)判断直线PD是否为⊙O的切线,并说明理由;
(2)如果∠BED=60°,PD=![]() ,求PA的长.
,求PA的长.
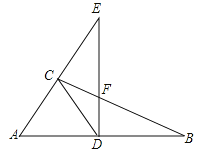
(3)将线段PD以直线AD为对称轴作对称线段DF,点F正好在圆O上,如图2,求证:四边形DFBE为菱形.
【答案】(1)直线PD为⊙O的切线,证明详见解析;(2)PA=1;(3)详见解析.
【解析】
(1)连接OD,由AB是圆O的直径可得∠ADB=90°,进而求得∠ADO+∠PDA=90°,即可得出直线PD为⊙O的切线;
(2)根据BE是⊙O的切线,则∠EBA=90°,即可求得∠P=30°,再由PD为⊙O的切线,得∠PDO=90°,根据三角函数的定义求得OD,由勾股定理得OP,即可得出PA;
(3)根据题意可证得∠ADF=∠PDA=∠PBD=∠ABF,由AB是圆O的直径,得∠ADB=90°,设∠PBD=x°,则可表示出∠DAF=∠PAD=90°+x°,∠DBF=2x°,由圆内接四边形的性质得出x的值,可得出△BDE是等边三角形.进而证出四边形DFBE为菱形.
(1)直线PD为⊙O的切线,
理由如下:
如图1,连接OD,

∵AB是圆O的直径,
∴∠ADB=90°,
∴∠ADO+∠BDO=90°,
又∵DO=BO,
∴∠BDO=∠PBD,
∵∠PDA=∠PBD,
∴∠BDO=∠PDA,
∴∠ADO+∠PDA=90°,即PD⊥OD,
∵点D在⊙O上,
∴直线PD为⊙O的切线;
(2)∵BE是⊙O的切线,
∴∠EBA=90°,
∵∠BED=60°,
∴∠P=30°,
∵PD为⊙O的切线,
∴∠PDO=90°,
在Rt△PDO中,∠P=30°,PD=![]() ,
,
∴![]() ,解得OD=1,
,解得OD=1,
∴![]() =2,
=2,
∴PA=PO﹣AO=2﹣1=1;
(3)如图2,
依题意得:∠ADF=∠PDA,∠PAD=∠DAF,
∵∠PDA=∠PBD∠ADF=∠ABF,
∴∠ADF=∠PDA=∠PBD=∠ABF,
∵AB是圆O的直径,
∴∠ADB=90°,
设∠PBD=x°,则∠DAF=∠PAD=90°+x°,∠DBF=2x°,
∵四边形AFBD内接于⊙O,
∴∠DAF+∠DBF=180°,
即90°+x+2x=180°,解得x=30°,
∴∠ADF=∠PDA=∠PBD=∠ABF=30°,
∵BE、ED是⊙O的切线,
∴DE=BE,∠EBA=90°,
∴∠DBE=60°,∴△BDE是等边三角形,
∴BD=DE=BE,
又∵∠FDB=∠ADB﹣∠ADF=90°﹣30°=60°∠DBF=2x°=60°,
∴△BDF是等边三角形,
∴BD=DF=BF,
∴DE=BE=DF=BF,
∴四边形DFBE为菱形.

【题目】在学校组织的“文明出行”知识竞赛中,8(1)和8(2)班参赛人数相同,成绩分为A、B、C三个等级,其中相应等级的得分依次记为A级100分、B级90分、C级80分,达到B级以上(含B级)为优秀,其中8(2)班有2人达到A级,将两个班的成绩整理并绘制成如下的统计图,请解答下列问题:
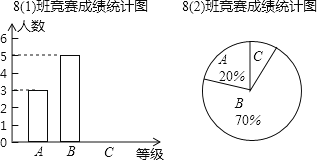
(1)求各班参赛人数,并补全条形统计图;
(2)此次竞赛中8(2)班成绩为C级的人数为_______人;
(3)小明同学根据以上信息制作了如下统计表:
平均数(分) | 中位数(分) | 方差 | |
8(1)班 | m | 90 | n |
8(2)班 | 91 | 90 | 29 |
请分别求出m和n的值,并从优秀率和稳定性方面比较两个班的成绩;