题目内容
如图，两个同心圆中，大圆的半径为2，∠AOB=120°，半径OE平分∠AOB，则图中阴影部分的面积为 ．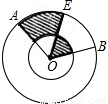
【答案】分析：通过整理可得阴影部分的面积=半径为2，圆心角为60°的扇形的面积．
解答：解：∵∠AOB=120°，半径OE平分∠AOB，
∴∠AOE=∠EOB=60°，阴影部分的面积等于扇形OAE的面积，
∴阴影扇形部分的面积=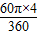
=
．
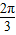所以，阴影部分的面积为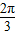
．
点评：本题利用了在同圆中弧相等，则弧对的圆心角相等，扇形的面积公式求解．
解答：解：∵∠AOB=120°，半径OE平分∠AOB，
∴∠AOE=∠EOB=60°，阴影部分的面积等于扇形OAE的面积，
∴阴影扇形部分的面积=
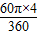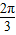=．所以，阴影部分的面积为
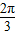．点评：本题利用了在同圆中弧相等，则弧对的圆心角相等，扇形的面积公式求解．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
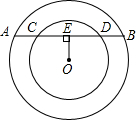如图，两个同心圆中，大圆的弦AB交小圆与点C、D，OE⊥AB垂足为E，且OE=1，若AB=4，CD=2，则两个同心圆的半径之比为（ ）| A、3：2 | ||||
B、
| ||||
C、
| ||||
| D、2：1 |
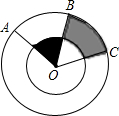如图，两个同心圆中，大圆的半径OA=4cm，∠AOB=∠BOC=60°，则图中阴影部分的面积是
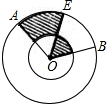如图，两个同心圆中，大圆的半径为2，∠AOB=120°，半径OE平分∠AOB，则图中阴影部分的面积为
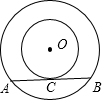如图，两个同心圆中，大圆的弦AB切小圆于点C，已知大圆的半径为5，小圆的半径为3，那么AB长是
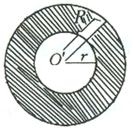3、如图，两个同心圆中，大圆半径R是小圆半径r的2倍，那么圆环面积（阴影部分）与小圆面积的比等于