题目内容
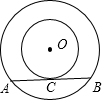 如图,两个同心圆中,大圆的弦AB切小圆于点C,已知大圆的半径为5,小圆的半径为3,那么AB长是
如图,两个同心圆中,大圆的弦AB切小圆于点C,已知大圆的半径为5,小圆的半径为3,那么AB长是分析:先连接OC,OB,由于AB是切线,那么∠OCB=90°,在Rt△OBC中利用勾股定理易求BC,再根据垂径定理可知AB=2BC,那么易求AB.
解答: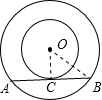 解:如右图所示,连接OC,OB,
解:如右图所示,连接OC,OB,
∵AB是切线,
∴∠OCB=90°,
又∵OC=3,OB=5,
∴BC=
=4,
∴AB=2BC=8,
故答案是8.
 解:如右图所示,连接OC,OB,
解:如右图所示,连接OC,OB,∵AB是切线,
∴∠OCB=90°,
又∵OC=3,OB=5,
∴BC=
| 52-32 |
∴AB=2BC=8,
故答案是8.
点评:本题考查了切线的性质、勾股定理、垂径定理.解题的关键是连接OC,OB,构造直角三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
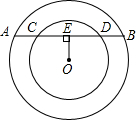 如图,两个同心圆中,大圆的弦AB交小圆与点C、D,OE⊥AB垂足为E,且OE=1,若AB=4,CD=2,则两个同心圆的半径之比为( )
如图,两个同心圆中,大圆的弦AB交小圆与点C、D,OE⊥AB垂足为E,且OE=1,若AB=4,CD=2,则两个同心圆的半径之比为( )| A、3:2 | ||||
B、
| ||||
C、
| ||||
| D、2:1 |
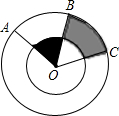 如图,两个同心圆中,大圆的半径OA=4cm,∠AOB=∠BOC=60°,则图中阴影部分的面积是
如图,两个同心圆中,大圆的半径OA=4cm,∠AOB=∠BOC=60°,则图中阴影部分的面积是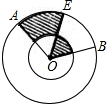 如图,两个同心圆中,大圆的半径为2,∠AOB=120°,半径OE平分∠AOB,则图中阴影部分的面积为
如图,两个同心圆中,大圆的半径为2,∠AOB=120°,半径OE平分∠AOB,则图中阴影部分的面积为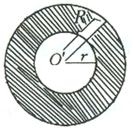 3、如图,两个同心圆中,大圆半径R是小圆半径r的2倍,那么圆环面积(阴影部分)与小圆面积的比等于
3、如图,两个同心圆中,大圆半径R是小圆半径r的2倍,那么圆环面积(阴影部分)与小圆面积的比等于