Question

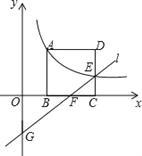
【题目】如图，正方形ABCD的顶点B，C在x轴的正半轴上，反比例函数（k≠0）在第一象限的图象经过顶点和CD边上的点，过点的直线交轴于点，交y轴于点G（0，﹣2），则点的坐标是__．

Answer 1

【答案】（2.25，0）

【解析】由点A（m，2）得到正方形的边长为2，则BC＝2，所以n=2+m，根据反比例图象上的坐标特征得到k=2m=（2+m），解得m=1，则E点坐标为（3， ），然后利用待定系数法确定直线GF的解析式为y=，再求y=0时对应自变量的值，从而得到点F的坐标．

解；方形的顶点A（m，2），
∴正方形的边长为2，
∴BC=2，而点E（n， ），
∴n=2+m，即E点坐标为（2+m， ），
∴k=2m=（2+m），解得m=1，
∴E点坐标为（3， ），
设直线GF的解析式为y=ax+b，
把E（3， ），G（0，-2）代入得，解得

∴直线GF的解析式为y=，
当y=0时， ＝0，

解得x=2.25，
∴点F的坐标为（2.25，0）．

“点睛”此题考查了反比例函数与一次函数的交点问题，涉及的知识有：待定系数法确定函数解析式，熟练掌握待定系数法是解本题的关键．