题目内容
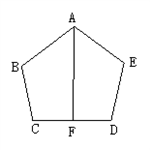
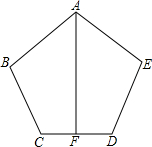 如图AB=AE,∠B=∠E,BC=ED,BC=ED,点F是CD的中点.
如图AB=AE,∠B=∠E,BC=ED,BC=ED,点F是CD的中点.(1)求证:AF⊥CD;
(2)若连接BE,请你直接写出三个新的结论.(无需证明)
分析:(1)连接AC、AD.根据SAS易证△ABC≌△AED,得AC=AD.根据等腰三角形三线合一性质可证结论;
(2)连接BE可得△ABE为等腰三角形.结合前面的证明可得AF垂直平分BE;CD∥BE;四边形BCDE是等腰梯形等结论.
(2)连接BE可得△ABE为等腰三角形.结合前面的证明可得AF垂直平分BE;CD∥BE;四边形BCDE是等腰梯形等结论.
解答: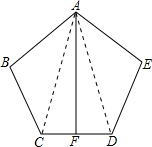 证明:连接AC、AD.
证明:连接AC、AD.
在△ABC与△AED中,
∴△ABC≌△AED.(SAS) (3分)
∴AC=AD.
∵点F是CD的中点,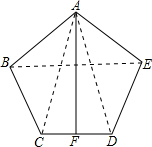
∴AF⊥CD; (5分)
(2)每写对一个得一分,(3分).
①AF垂直平分BE;②CD∥BE;③四边形BCDE是等腰梯形.
 证明:连接AC、AD.
证明:连接AC、AD.在△ABC与△AED中,
|
∴△ABC≌△AED.(SAS) (3分)
∴AC=AD.
∵点F是CD的中点,

∴AF⊥CD; (5分)
(2)每写对一个得一分,(3分).
①AF垂直平分BE;②CD∥BE;③四边形BCDE是等腰梯形.
点评:此题考查全等三角形的判定和性质及等腰三角形的性质,添加辅助线构造全等三角形是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
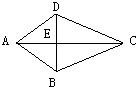 如图AB=AD,BC=CD,AC与BD相交于E,由这些条件你能推出哪些结论(不再添加辅助线,不再标注其他字母,不写推理过程,只要求写出四个你认为正确的结论
如图AB=AD,BC=CD,AC与BD相交于E,由这些条件你能推出哪些结论(不再添加辅助线,不再标注其他字母,不写推理过程,只要求写出四个你认为正确的结论
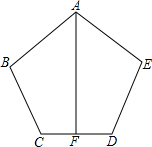 如图AB=AE,∠B=∠E,BC=ED,BC=ED,点F是CD的中点.
如图AB=AE,∠B=∠E,BC=ED,BC=ED,点F是CD的中点.