题目内容
已知: 如图,AB=AE,BC=ED, ∠B= ∠E,AF ⊥CD,F 为垂足, 求证:CF=DF.
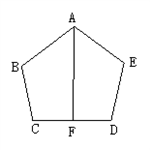
解：连结AC 、AD,
则在△ABC 和△AED 中有
∴△ABC≌△AED
∴AC=AD
又∵AF⊥CD
∴∠AFC=∠AFD=90°
又∵在Rt△ACF和Rt△ADF中有
∴Rt△ACF≌Rt△ADF∴CF=DF
则在△ABC 和△AED 中有
∴△ABC≌△AED
∴AC=AD
又∵AF⊥CD
∴∠AFC=∠AFD=90°
又∵在Rt△ACF和Rt△ADF中有
∴Rt△ACF≌Rt△ADF∴CF=DF
练习册系列答案
相关题目
已知：如图AB∥CD，∠1=∠A，∠2=∠C，B、E、D在一条直线上．
19、已知，如图AB=DE，BD=CF，AC=EF
已知：如图AB是半圆0的直径，点C在半圆上，CD⊥AB，垂足为D，切线PC交BA的延长线于点P，AD，DB的长是关于x的方程x2-（4m+2）+4m2=0（m＞0）的两根，且AD：DB=1：4，求：PO、PC的长．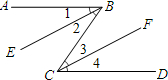
已知：如图AB∥CD，BE∥CF．试说明：∠1=∠4．
已知：如图AB∥CD，CE平分∠ACD，∠A=110°，则∠ECD等于