题目内容
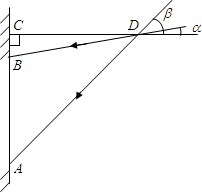（2013•宝安区二模）在课题学习后，同学们为教室窗户设计一个遮阳蓬，小明同学绘制的设计图如图所示，其中，AB表示窗户，且AB=2.82米，△BCD表示直角遮阳蓬，已知当地一年中在午时的太阳光与水平线CD的最小夹角α为18°，最大夹角β为66°，根据以上数据，计算出遮阳蓬中CD的长是（结果精确到0.1）（参考数据：sin18°≈0.31，tan18°≈0.32，sin66°≈0.91，tan66°≈2.2）（ ）分析：如图所示，假设CD为x，则有在Rt△BCD中可利用tan∠BDC=
得到BC=CD•tan∠BDC=0.32x，在Rt△ACD中利用tan∠ADC=
，得到AC=CD•tan∠ADC=2.2x，则AB=AC-BC，列方程可得
2.82=2.2x-0.32x，解得x的值即可．
| BC |
| CD |
| AC |
| CD |
2.82=2.2x-0.32x，解得x的值即可．
解答：解：设CD为x，
在Rt△BCD中，∠BDC=α=18.6°，
∵tan∠BDC=
，
∴BC=CD•tan∠BDC=0.32x，
在Rt△ACD中，∠ADC=β=64.5°，
∵tan∠ADC=
，
∴AC=CD•tan∠ADC=2.2x，
∵AB=AC-BC，
∴2.82=2.2x-0.32x，
解得：x=1.5．
答：CD长约为1.5米．
故选：B．
解：设CD为x，在Rt△BCD中，∠BDC=α=18.6°，
∵tan∠BDC=
| BC |
| CD |
∴BC=CD•tan∠BDC=0.32x，
在Rt△ACD中，∠ADC=β=64.5°，
∵tan∠ADC=
| AC |
| CD |
∴AC=CD•tan∠ADC=2.2x，
∵AB=AC-BC，
∴2.82=2.2x-0.32x，
解得：x=1.5．
答：CD长约为1.5米．
故选：B．
点评：本题考查解直角三角形的应用，解此题关键是把实际问题转化为数学问题，本题只要把实际问题抽象到三角形中，根据线段之间的转换列方程即可．注意实际问题要入进．
练习册系列答案
相关题目
（2013•宝安区二模）如图，在矩形ABCD中，AB=3，BC=9，把矩形ABCD沿对角线BD折叠，使点C与点F重合，BF交AD于点M，过点C作CE⊥BF于点E，交AD于点G，则MG的长=