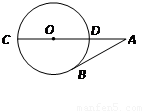题目内容
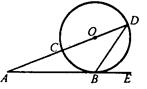
如图，CD是⊙O的切线，D是直径AB的延长线上一点，∠D=30°，则∠BAC=________°．
30
分析：连接OC，根据切线得出∠OCD=90°，求出∠COD，求出∠OCA=∠BAC，根据三角形的外角性质即可求出答案．
解答：
连接OC，
∵CD是⊙O的切线，
∴∠OCD=90°，
∵∠D=30°，
∴∠COD=60°，
∵OC=OA，
∴∠BAC=∠OCA，
∵∠BAC+∠OCA=∠COD=60°，
∴∠BAC=30°，
故答案为：30．
点评：本题考查了三角形的内角和定理，切线性质，三角形的外角性质，等腰三角形的性质的应用，关键是正确作辅助线，并进一步求出∠COD的度数，题目具有一定的代表性，是一道比较好的题目．
分析：连接OC，根据切线得出∠OCD=90°，求出∠COD，求出∠OCA=∠BAC，根据三角形的外角性质即可求出答案．
解答：
连接OC，∵CD是⊙O的切线，
∴∠OCD=90°，
∵∠D=30°，
∴∠COD=60°，
∵OC=OA，
∴∠BAC=∠OCA，
∵∠BAC+∠OCA=∠COD=60°，
∴∠BAC=30°，
故答案为：30．
点评：本题考查了三角形的内角和定理，切线性质，三角形的外角性质，等腰三角形的性质的应用，关键是正确作辅助线，并进一步求出∠COD的度数，题目具有一定的代表性，是一道比较好的题目．
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
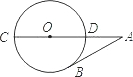已知：如图，CD是⊙O的直径，点A在CD的延长线上，AB切⊙O于点B，若∠A=30°，OA=10，则AB=
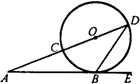1、已知：如图，CD是⊙O的直径，AE切⊙O于点B，DC的延长线交AB于点A，∠A=20°，则∠DBE=
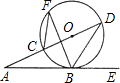2cm．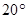
，则∠DBE＝_________； 
