题目内容
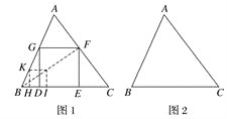
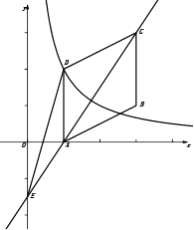
【题目】（本题12分）如图，抛物线
交
轴正半轴于点A，顶点为M，对称轴NB交轴于点B，过点C（2，0）作射线CD交MB于点D（D在轴上方），OE∥CD交MB于点E，EF∥轴交CD于点F，作直线MF。
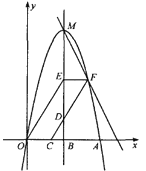
（1）求点A，M的坐标；
（2）当BD为何值时，点F恰好落在抛物线上？
（3）当BD=1时，①、求直线MF的解析式，并判断点A是否落在该直线上；
②、延长OE交FM于点G，取CF中点P，连结PG，△FPG，四边形DEGP，四边形OCDE的面积分别记为S1，S2，S3，则S1:S2:S3=
【答案】A（6,0）M（3,9）；BD=
；见解析；3:4:8.
【解析】试题（1）令y=0求出x的解，从而得到点A的坐标，根据抛物线的顶点坐标求法得出点M的坐标；（2）根据OE∥CF，OC∥EF，C（2,0）得出EF=OC=2，则BC=1，根据点F的横坐标以及抛物线的解析式求出点F的坐标，从而得出BE的长度，根据
得出DE=2BD，则BE=3BD，求出BD的长度；（3）。当BD=1时，得出点F的坐标，然后设MF的解析式为y=kx+b，将点M和点F代入解析式求出函数解析式，然后将x=6代入直线解析式看y是否为零，分别求出三个图形的面积，然后得出比值.
试题解析：（1）令y=0，则－
+6x=0，解得： 
=0， 
=6 ∴A（6,0） ∴对称轴是直线x=3 ∴M（3,9）
（2）∵OE∥CF，OC∥EF，C（2,0） ∴EF=OC=2 ∴BC=1 ∴点F的横坐标为5
∵点F落在抛物线上 ∴F（5,5），BE=5 ∵
∴DE=2BD
∴BE=3BD ∴BD=
（3）①当BD=1时，BE="3" ∴F（5,3） 设MF的解析式为y=kx+b
将点M和点F代入得： 
解得： 
∴y=－3x+18
当x=6时，y=－3×6+18=0 ∴点A落在直线MF上
②、3:4:8
