Question

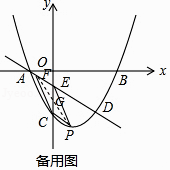
【题目】如图，抛物线y= x2+bx+c经过点B（3，0），C（0，﹣2），直线l：y=﹣ x﹣ 交y轴于点E，且与抛物线交于A，D两点，P为抛物线上一动点（不与A，D重合）．

（1）求抛物线的解析式；
（2）当点P在直线l下方时，过点P作PM∥x轴交l于点M，PN∥y轴交l于点N，求PM+PN的最大值．
（3）设F为直线l上的点，以E，C，P，F为顶点的四边形能否构成平行四边形？若能，求出点F的坐标；若不能，请说明理由．

Answer 1

【答案】
（1）

解：把B（3，0），C（0，﹣2）代入y= x2+bx+c得， ，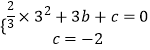

∴

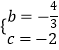
∴抛物线的解析式为：y= x2﹣ x﹣2

（2）

解：设P（m， m2﹣ m﹣2），

∵PM∥x轴，PN∥y轴，M，N在直线AD上，

∴N（m，﹣ m﹣ ），M（﹣m2+2m+2， m2﹣ m﹣2），

∴PM+PN=﹣m2+2m+2﹣m﹣ m﹣ ﹣ m2+ m+2=﹣ m2+ m+ =﹣ （m﹣ ）2+ ，

∴当m= 时，PM+PN的最大值是

（3）

解：能，

理由：∵y=﹣ x﹣ 交y轴于点E，

∴E（0，﹣ ），

∴CE= ，

设P（m， m2﹣ m﹣2），

∵以E，C，P，F为顶点的四边形能否构成平行四边形，

①以CE为边，∴CE∥PF，CE=PF，

∴F（m，﹣ m﹣ ），

∴﹣ m﹣ ﹣ m2+ m+2= ，

∴m=1，m=0（舍去），

②以CE为对角线，连接PF交CE于G，

∴CG=GE，PG=FG，

∴G（0，﹣ ），

设P（m， m2﹣ m﹣2），则F（﹣m， m﹣ ），

∴ ×（ m2﹣ m﹣2+ m﹣ ）=﹣ ，

∵△＜0，

∴此方程无实数根，

综上所述，当m=1时，以E，C，P，F为顶点的四边形能否构成平行四边形．

【解析】（1.）把B（3，0），C（0，﹣2）代入y= x2+bx+c解方程组即可得到结论；（2.）设P（m， m2﹣ m﹣2），得到N（m，﹣ m﹣ ），M（﹣m2+2m+2， m2﹣ m﹣2），根据二次函数的性质即可得到结论；
（3.）求得E（0，﹣ ），得到CE= ，设P（m， m2﹣ m﹣2），①以CE为边，根据CE=PF，列方程得到m=1，m=0（舍去），②以CE为对角线，连接PF交CE于G，CG=GE，PG=FG，得到G（0，﹣ ），设P（m， m2﹣ m﹣2），则F（﹣m， m﹣ ），列方程得到此方程无实数根，于是得到结论．
【考点精析】解答此题的关键在于理解求根公式的相关知识，掌握根的判别式△=b2-4ac，这里可以分为3种情况：1、当△>0时，一元二次方程有2个不相等的实数根2、当△=0时，一元二次方程有2个相同的实数根3、当△<0时，一元二次方程没有实数根，以及对二次函数的性质的理解，了解增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．