��Ŀ����
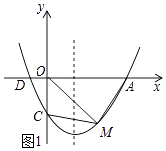
����Ŀ����ͼ�����κ���y=ax2+bx+c��ͼ����x��Ľ���ΪA��D��A��D���Ҳࣩ����y��Ľ���ΪC����A��4��0����C��0����3�����Գ�����ֱ��x=1��
��1������κ����Ľ���ʽ��
��2����M�ǵ���������������һ���㣬�Һ�����Ϊm�����ı���OCMA�����Ϊs����д��s��m֮��ĺ�����ϵʽ���������mΪ��ֵʱ���ı���OCMA��������
��3�����B��x���ϵĵ㣬P���������ϵĵ㣬�Ƿ���ڵ�P��ʹ����A��B��C��P�ĵ�Ϊ������ı���Ϊƽ���ı��Σ������ڣ�ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺��A��4��0�����Գ�����ֱ��x=l��
��D����2��0����
�֡�C��0����3��
�� 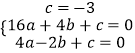
��ã�a= ![]() ��b=��
��b=�� ![]() ��c=��3��
��c=��3��
����κ�������ʽΪ��y= ![]() x2��
x2�� ![]() x��3��
x��3��
��2��
�⣺��ͼ1��ʾ��
��M��m�� ![]() x2��
x2�� ![]() x��3����|yM|=��
x��3����|yM|=�� ![]() m2+
m2+ ![]() m+3��
m+3��
��S=S��ACM+S��OAM
��S= ![]() ��OC��m+
��OC��m+ ![]() ��OA��|yM|=
��OA��|yM|= ![]() ��3��m+
��3��m+ ![]() ��4������
��4������ ![]() m2+
m2+ ![]() m+3��=��
m+3��=�� ![]() m2+3m+6=��
m2+3m+6=�� ![]() ��m��2��2+9��
��m��2��2+9��
��m=2ʱ��s�����9��
��3��
�⣺��ABΪƽ���ı��εı�ʱ����AB��PC��
��PC��x�ᣮ
���P����������3��
��y=��3����ã� ![]() x2��
x2�� ![]() x��3=��3����ã�x=0��x=2��
x��3=��3����ã�x=0��x=2��
���P��������2����3����
��ABΪ�Խ���ʱ��
��ABCPΪƽ���ı��Σ�
��AB��CP����ƽ�֣�
���P��������Ϊ3��
��y=3����ã� ![]() x2��
x2�� ![]() x��3=3�������ã�x2��2x��16=0����ã�x=1+
x��3=3�������ã�x2��2x��16=0����ã�x=1+ ![]() ��x=1��
��x=1�� ![]() ��
��
�������������ڵ�P��2����3����P��1+ ![]() ��3����P��1��
��3����P��1�� ![]() ��3��ʹ����A��B��C��P�ĵ�Ϊ������ı���Ϊƽ���ı��Σ�
��3��ʹ����A��B��C��P�ĵ�Ϊ������ı���Ϊƽ���ı��Σ�
����������1�����������ߵĶԳ��Կɵõ���D���ܱ���Ȼ��A��C��D��������������ߵĽ���ʽ�����a��b��c��ֵ���Ӷ��ɵõ����κ����Ľ���ʽ����2����M��m�� ![]() x2��
x2�� ![]() x��3����|yM|=��
x��3����|yM|=�� ![]() m2+
m2+ ![]() m+3����S=S��ACM+S��OAM�ɵõ�S��m�ĺ�����ϵʽ��Ȼ�������䷽�������S�����ֵ����3����ABΪƽ���ı��εı�ʱ����AB��PC�����P��������Ϊ��3����y=��3���������ߵĽ���ʽ����õ�P�ĺ����ꣻ��ABΪ�Խ���ʱ��AB��CP����ƽ�֣����P��������Ϊ3����y=3���������ߵĽ���ʽ����õ�P�ĺ����꣮
m+3����S=S��ACM+S��OAM�ɵõ�S��m�ĺ�����ϵʽ��Ȼ�������䷽�������S�����ֵ����3����ABΪƽ���ı��εı�ʱ����AB��PC�����P��������Ϊ��3����y=��3���������ߵĽ���ʽ����õ�P�ĺ����ꣻ��ABΪ�Խ���ʱ��AB��CP����ƽ�֣����P��������Ϊ3����y=3���������ߵĽ���ʽ����õ�P�ĺ����꣮
�����㾫����������Ĺؼ�����������κ��������ʵ����֪ʶ�����������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��

 �����������һ��һ��ϵ�д�
�����������һ��һ��ϵ�д� Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д�



