题目内容
【题目】如图，已知E、F、G、H是四边形ABCD四边的中点，则四边形EFGH的形状为_____；如四边形ABCD的对角线AC 与BD的和为40，则四边形EFGH的周长为________.
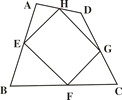
【答案】平行四边形； 40
【解析】
利用三角形的中位线定理求出四边形EFGH的两组对边相等，即可证得四边形EFGH是平行四边形，继而即可求得EFGH的周长．
解：连接AC、BD，
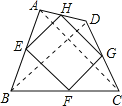
∵E、F、G、H分别为四边形ABCD四边的中点，
∴EH=
BD，FG=BD，HG=AC，EF=AC，
∴EH=FG，EF=HG，
∴四边形EFGH是平行四边形．
∴四边形EFGH的周长=EH+HG+FG+EF=×2×AC+×2×BD=AC+BD=40．
故答案为：平行四边形；40．
练习册系列答案
名校课堂系列答案
相关题目
【题目】李辉到服装专卖店去做社会调查，了解到商店为了激励营业员的工作积极性实行了“月总收入=基本工资+计件奖金”的方法，并获得了如下信息：
营业员 | 嘉琪 | 嘉善 |
月销售件数/件 | 400 | 300 |
月总收入/元 | 7800 | 6600 |
假设月销售件数为x件，月总收入为y元，销售每件奖励a元，营业员月基本工资为b元．
（1）求a、b的值．
（2）若营业员嘉善某月总收入不低于4200元，那么嘉善当月至少要卖多少件衣服？
