Question

【题目】如图，小明在大楼30米高（即PH＝30米）的窗口P处进行观测，测得山坡上A处的俯角为15°，山脚B处的俯角为60°，已知该山坡的坡度i（即tan∠ABC）为1∶，点P、H、B、C、A在同一平面上，点H、B、C在同一条直线上，且PH⊥HC，

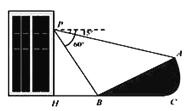
（1）山坡坡角（即∠ABC）的度数等于 度.

（2）求A、B两点间的距离（结果精确到0.1米.参考数据≈1.732）

Answer 1

【答案】(1)、30°；(2)、34.6米.

【解析】

试题分析：(1)、根据坡度i的值得出∠ABC的角度大小；(2)、首先根据Rt△BHP得出PB的长度，然后得出△ABP为等腰直角三角形，然后求出AP的长度.

试题解析：(1)、∵i=1： ∴∠ABC=30°

(2)、在Rt△BHP中，∠PBH=600， ∵=sin∠PBH，∴PB==20

在△ABP中，∠APB=60°-15°=45°， ∠ABP=180°－∠PBH－∠ABC=180°－60°－30°=90°

∴△ABP是等腰直角三角形，∴AB=PB=20≈34.6（米）

答：A、B两点间的距离约为34.6米.